Rumus Tinggi Persegi Panjang Panduan Lengkap

Rumus tinggi persegi panjang? Eh, tunggu dulu! Bukannya persegi panjang nggak punya tinggi ya? Tenang, kita akan mengupas tuntas misteri ini. Soalnya, kalau kita bicara soal bangun ruang yang dasarnya persegi panjang, baru deh ada tingginya. Bayangkan saja balok, kotak kado, atau bahkan gedung pencakar langit—semuanya punya tinggi yang bisa kita hitung! Siap-siap kuasai rumus dan aplikasinya dalam kehidupan sehari-hari, dari menghitung ubin lantai sampai mendesain rumah impian!

Persegi panjang, bangun datar yang familiar dengan sisi-sisi sejajar dan sudut siku-siku, ternyata menyimpan banyak rahasia. Memahami rumus luas dan kelilingnya adalah kunci untuk menguasai berbagai perhitungan geometri. Lebih dari itu, penguasaan ini akan sangat berguna dalam berbagai aplikasi praktis, mulai dari arsitektur hingga desain grafis. Artikel ini akan membahas secara detail rumus-rumus tersebut, lengkap dengan contoh soal dan penerapannya dalam kehidupan nyata. Siap menjelajahi dunia geometri yang menarik?

Pengertian Persegi Panjang

Persegi panjang? Bentuk geometris yang akrab banget, ya! Dari buku, layar HP, sampai lapangan bola, kita ketemu bentuk ini setiap hari. Tapi, apa sih sebenarnya definisi formalnya? Yuk, kita bahas tuntas!

Secara formal, persegi panjang adalah bangun datar dua dimensi yang memiliki empat sisi dan empat sudut. Syarat utamanya? Sisi-sisi yang berhadapan harus sejajar dan sama panjang, sementara keempat sudutnya harus siku-siku (90 derajat). Dalam geometri analitik, persegi panjang bisa direpresentasikan sebagai himpunan titik-titik yang memenuhi persamaan tertentu, tergantung bagaimana kita mendefinisikan koordinat titik sudutnya.

Contoh Persegi Panjang dalam Kehidupan Sehari-hari

Persegi panjang bukan cuma teori di buku geometri, lho! Bentuk ini sering banget kita temui dalam kehidupan nyata. Berikut beberapa contohnya:

• Layar komputer/HP: Bentuk layar gadget kita umumnya persegi panjang. Rasio aspeknya (perbandingan lebar dan tinggi) bisa bervariasi, tapi tetap memenuhi syarat sisi berhadapan sejajar dan sama panjang, serta sudut siku-siku.
• Lembar kertas: Baik kertas A4 maupun jenis lainnya, umumnya berbentuk persegi panjang. Ukurannya memang berbeda-beda, tetapi tetap mengikuti definisi persegi panjang.
• Pintu dan Jendela: Kebanyakan pintu dan jendela rumah atau bangunan dirancang berbentuk persegi panjang untuk efisiensi dan estetika.
• Lapangan Bola Basket: Lapangan bola basket standar berbentuk persegi panjang dengan ukuran tertentu, memastikan permainan berjalan dengan standar yang sama di berbagai tempat.
• Batu Bata: Batu bata yang digunakan dalam konstruksi bangunan umumnya berbentuk persegi panjang, memudahkan proses penataan dan pemasangannya.

Perbandingan Persegi Panjang dengan Bangun Datar Lainnya

Supaya lebih jelas, mari kita bandingkan persegi panjang dengan bangun datar lainnya. Perbedaannya terletak pada sifat sudut dan sisi.

Nama Bangun Datar	Sifat Sudut	Sifat Sisi	Rumus Luas	Rumus Keliling
Persegi Panjang	Keempat sudut siku-siku (90 derajat)	Sisi berhadapan sejajar dan sama panjang	panjang x lebar	2 x (panjang + lebar)
Persegi	Keempat sudut siku-siku (90 derajat)	Keempat sisi sama panjang	sisi x sisi	4 x sisi
Jajargenjang	Sudut berhadapan sama besar	Sisi berhadapan sejajar dan sama panjang	alas x tinggi	2 x (panjang + lebar)
Belah Ketupat	Sudut berhadapan sama besar	Keempat sisi sama panjang	1/2 x diagonal1 x diagonal2	4 x sisi

Perbedaan Persegi Panjang dan Persegi

Meskipun sekilas mirip, persegi panjang dan persegi punya perbedaan yang cukup signifikan:

• Panjang Sisi: Persegi memiliki keempat sisi sama panjang, sedangkan persegi panjang hanya sisi berhadapan yang sama panjang.
• Kebebasan Bentuk: Persegi hanya memiliki satu bentuk, sementara persegi panjang bisa memiliki berbagai bentuk dengan perbandingan panjang dan lebar yang berbeda-beda.
• Kriteria Khusus: Persegi merupakan kasus khusus dari persegi panjang dimana semua sisinya sama panjang.

Karakteristik Utama Persegi Panjang

Ada beberapa karakteristik kunci yang membedakan persegi panjang dari bangun datar lainnya:

• Empat Sisi dan Empat Sudut: Ini merupakan ciri dasar bangun datar segi empat.
• Sudut Siku-Siku: Keempat sudutnya selalu 90 derajat.
• Sisi Berhadapan Sejajar dan Sama Panjang: Ini yang membedakannya dari jajargenjang (hanya sisi berhadapan yang sejajar).
• Diagonal yang Sama Panjang dan Saling Membagi Dua: Diagonal-diagonalnya membagi persegi panjang menjadi dua segitiga kongruen.
• Memiliki Dua Sumbu Simetri: Garis yang membagi dua sisi berhadapan.

Rumus Menghitung Luas Persegi Panjang

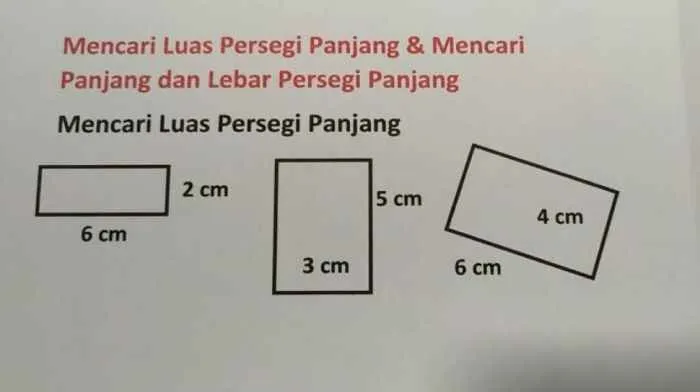
Persegi panjang, bangun datar yang akrab kita temui sehari-hari, ternyata menyimpan rumus sederhana namun ampuh untuk menghitung luasnya. Dari menghitung luas lantai rumah hingga mendesain taman minimalis, rumus ini jadi kunci utamanya! Yuk, kita bongkar rahasia menghitung luas persegi panjang!

Rumus Luas Persegi Panjang dan Contoh Perhitungan

Rumus luas persegi panjang itu simpel banget, kok! Cukup kalikan panjang dengan lebarnya. Secara matematis, bisa ditulis begini:

Luas = Panjang x Lebar

Misalnya, kita punya persegi panjang dengan panjang 10 cm dan lebar 5 cm. Maka luasnya adalah:

Luas = 10 cm x 5 cm = 50 cm²

Gampang, kan? Satuan luas selalu kuadrat (cm², m², dll.) karena kita mengalikan dua besaran panjang.

Contoh Soal dan Penyelesaian Luas Persegi Panjang

Berikut tiga contoh soal yang akan mengasah pemahamanmu tentang perhitungan luas persegi panjang:

1. Sebuah halaman rumah berbentuk persegi panjang dengan panjang 12 meter dan lebar 8 meter. Berapa luas halaman tersebut?
2. Sebuah lukisan berukuran panjang 50 cm dan lebar 30 cm. Berapakah luas lukisan tersebut?
3. Sebuah lapangan sepak bola memiliki panjang 100 meter dan lebar 70 meter. Tentukan luas lapangan tersebut.

Penyelesaian:

1. Luas = 12 m x 8 m = 96 m²
2. Luas = 50 cm x 30 cm = 1500 cm²
3. Luas = 100 m x 70 m = 7000 m²

Ilustrasi Persegi Panjang dan Perhitungan Luas

Bayangkan sebuah persegi panjang yang mewakili sebuah kolam renang mini. Kolam tersebut memiliki panjang 4 meter dan lebar 2 meter. Kita bisa menggambarnya seperti ini (dalam pikiran ya, karena kita tidak pakai gambar):

Gambarlah persegi panjang dengan panjang 4 meter dan lebar 2 meter. Tuliskan angka 4 meter di sisi panjang dan 2 meter di sisi lebar. Kemudian, hitung luasnya:

Luas = 4 m x 2 m = 8 m²

Jadi, luas kolam renang mini tersebut adalah 8 meter persegi.

Menghitung Luas Persegi Panjang jika Diketahui Keliling dan Salah Satu Sisi

Kalau yang diketahui cuma keliling dan salah satu sisi? Tenang, tetap bisa dihitung! Ingat rumus keliling persegi panjang: Keliling = 2 x (Panjang + Lebar). Dari sini, kita bisa cari sisi yang belum diketahui, baru deh hitung luasnya.

Misalnya, keliling persegi panjang 20 cm dan panjangnya 7 cm. Maka:

1. 20 cm = 2 x (7 cm + Lebar)
2. 10 cm = 7 cm + Lebar
3. Lebar = 3 cm

Sekarang kita bisa hitung luasnya:

Luas = 7 cm x 3 cm = 21 cm²

Langkah-langkah Menghitung Luas Persegi Panjang

Untuk memastikan perhitunganmu akurat dan efisien, ikuti langkah-langkah berikut:

1. Tentukan panjang dan lebar persegi panjang.
2. Masukkan nilai panjang dan lebar ke dalam rumus Luas = Panjang x Lebar.
3. Kalikan panjang dan lebar.
4. Tambahkan satuan luas (cm², m², dll.) pada hasil perhitungan.

Rumus Menghitung Keliling Persegi Panjang

Keliling persegi panjang? Gak cuma buat pelajaran Matematika aja, lho! Konsep ini sering banget kita pakai dalam kehidupan sehari-hari, mulai dari ngukur kain buat bikin baju sampai mendesain taman rumah. Paham rumusnya? Yuk, kita bahas tuntas!

Persegi panjang, bangun datar yang punya dua pasang sisi sejajar dan sama panjang, punya rumus keliling yang simpel dan mudah diingat. Rumus ini didapatkan dari menjumlahkan panjang semua sisi-sisinya. Karena persegi panjang punya dua pasang sisi yang sama panjang, maka rumus kelilingnya bisa disingkat.

Rumus Keliling Persegi Panjang dan Contoh Perhitungan

Rumus keliling persegi panjang adalah:

K = 2(p + l)

di mana:

• K = Keliling persegi panjang
• p = Panjang persegi panjang
• l = Lebar persegi panjang

Rumus ini berlaku karena keliling adalah total panjang sisi-sisi yang membatasi bangun datar. Sifat persegi panjang yang memiliki sisi-sisi berpasangan sama panjang memudahkan perhitungan menjadi lebih efisien.

Contoh 1 (Bilangan Bulat):

Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Hitung kelilingnya!

Penyelesaian:

1. K = 2(p + l)
2. K = 2(10 cm + 5 cm)
3. K = 2(15 cm)
4. K = 30 cm

Jadi, keliling persegi panjang tersebut adalah 30 cm.

Contoh 2 (Bilangan Desimal):

Sebuah persegi panjang memiliki panjang 7.5 cm dan lebar 3.2 cm. Hitung kelilingnya!

Penyelesaian:

1. K = 2(p + l)
2. K = 2(7.5 cm + 3.2 cm)
3. K = 2(10.7 cm)
4. K = 21.4 cm

Jadi, keliling persegi panjang tersebut adalah 21.4 cm.

Contoh Soal Keliling Persegi Panjang

Berikut tiga contoh soal dengan tingkat kesulitan berbeda:

1. Mudah: Sebuah persegi panjang memiliki panjang 8 cm dan lebar 6 cm. Berapa kelilingnya?
2. Sedang: Sebuah lapangan berbentuk persegi panjang memiliki keliling 48 meter. Jika panjang lapangan 14 meter, berapakah lebarnya?
3. Sulit: Sebuah taman berbentuk persegi panjang memiliki panjang 2 1/2 meter dan lebar 1,5 meter. Berapa keliling taman tersebut dalam sentimeter?

Penyelesaian soal-soal tersebut akan melibatkan penerapan rumus keliling persegi panjang dan langkah-langkah perhitungan yang sistematis. Untuk soal sulit, akan diperlukan konversi satuan meter ke sentimeter.

Ilustrasi Persegi Panjang dan Perhitungan Keliling

Bayangkan sebuah persegi panjang dengan panjang 12 cm dan lebar 8 cm. Kita bisa mengilustrasikan persegi panjang ini dengan gambar. Gambar tersebut akan menunjukkan persegi panjang dengan panjang 12 cm dan lebar 8 cm yang diberi label. Di samping gambar, akan tertera perhitungan kelilingnya sebagai berikut:

K = 2 (p + l) = 2 (12 cm + 8 cm) = 2 (20 cm) = 40 cm

Jadi, keliling persegi panjang tersebut adalah 40 cm.

Perbandingan Rumus Keliling Berbagai Bangun Datar

Berikut tabel perbandingan rumus keliling persegi panjang, persegi, dan segitiga:

Bangun Datar	Rumus Keliling	Penjelasan Singkat	Contoh Perhitungan
Persegi Panjang	K = 2(p + l)	Jumlah dua kali panjang ditambah lebar	K = 2(10 + 5) = 30
Persegi	K = 4s	Empat kali panjang sisi	K = 4(7) = 28
Segitiga	K = a + b + c	Jumlah ketiga sisi	K = 5 + 6 + 7 = 18

Perbedaan utama terletak pada jumlah sisi dan apakah sisi-sisi tersebut memiliki panjang yang sama atau berbeda.

Langkah-Langkah Menghitung Keliling Persegi Panjang (Flowchart)

Berikut langkah-langkah menghitung keliling persegi panjang yang disajikan dalam bentuk deskripsi, karena pembuatan flowchart membutuhkan alat bantu visual yang berada di luar kemampuan penulisan teks ini.

1. Tentukan panjang (p) dan lebar (l) persegi panjang.
2. Jumlahkan panjang dan lebar: p + l.
3. Kalikan hasil penjumlahan dengan 2: 2(p + l).
4. Hasilnya adalah keliling persegi panjang (K).

Soal Cerita Keliling Persegi Panjang

Bu Ani ingin memasang pagar di sekeliling kebunnya yang berbentuk persegi panjang. Panjang kebun 15 meter dan lebarnya 10 meter. Berapa panjang pagar yang dibutuhkan Bu Ani?

Penyelesaian: Keliling kebun = 2 (panjang + lebar) = 2 (15 m + 10 m) = 50 m. Jadi, Bu Ani membutuhkan pagar sepanjang 50 meter.

Rumus Keliling Persegi Panjang dalam Python

Berikut kode Python untuk menghitung keliling persegi panjang:

# Fungsi untuk menghitung keliling persegi panjang
def keliling_persegi_panjang(panjang, lebar):
  """
  Fungsi ini menghitung keliling persegi panjang.

  Args:
    panjang: Panjang persegi panjang.
    lebar: Lebar persegi panjang.

  Returns:
    Keliling persegi panjang.
  """
  keliling = 2 * (panjang + lebar)
  return keliling

# Mendapatkan input dari pengguna
panjang = float(input("Masukkan panjang persegi panjang: "))
lebar = float(input("Masukkan lebar persegi panjang: "))

# Menghitung dan menampilkan keliling
keliling = keliling_persegi_panjang(panjang, lebar)
print("Keliling persegi panjang adalah:", keliling)

Hubungan Antara Luas dan Keliling Persegi Panjang

Persegi panjang, bangun datar yang akrab kita temui sehari-hari, menyimpan rahasia menarik dalam hubungan antara luas dan kelilingnya. Lebih dari sekadar rumus, memahami hubungan ini membuka pintu untuk memecahkan berbagai masalah, dari mendesain kandang ayam hingga merencanakan tata ruang rumah. Yuk, kita kupas tuntas!

Pengertian dan Rumus Luas dan Keliling Persegi Panjang

Sebelum menyelami hubungannya, kita perlu mengingat kembali definisi dan rumus masing-masing. Luas persegi panjang adalah ukuran area yang ditempatinya, sementara keliling adalah total panjang sisi-sisinya. Bayangkan kamu mau ngecat dinding kamar, luasnya menentukan berapa banyak cat yang dibutuhkan, sedangkan kelilingnya menentukan panjang lisplank yang diperlukan.

• Luas Persegi Panjang: Luas dihitung dengan mengalikan panjang dan lebarnya. Rumusnya adalah:
  

  $L = p \times l$

  , di mana L adalah luas, p adalah panjang, dan l adalah lebar.

• Keliling Persegi Panjang: Keliling dihitung dengan menjumlahkan semua sisi-sisinya. Rumusnya adalah:
  

  $K = 2(p + l)$

  , di mana K adalah keliling, p adalah panjang, dan l adalah lebar.

Hubungan Matematis Luas dan Keliling Persegi Panjang

Luas dan keliling persegi panjang punya hubungan yang menarik, yaitu tidak langsung proporsional. Artinya, perubahan pada satu besaran tidak secara otomatis menyebabkan perubahan yang sebanding pada besaran lainnya. Misalnya, persegi panjang dengan panjang 10 cm dan lebar 5 cm memiliki luas 50 cm² dan keliling 30 cm. Jika kita gandakan panjangnya menjadi 20 cm, luasnya menjadi 100 cm², tetapi kelilingnya hanya menjadi 50 cm. Perubahan luas lebih signifikan daripada perubahan keliling.

Perubahan Panjang dan Lebar serta Pengaruhnya terhadap Luas dan Keliling

Mari kita lihat bagaimana perubahan proporsional pada panjang dan lebar mempengaruhi luas dan keliling. Tabel berikut memberikan gambaran yang lebih jelas:

Panjang (cm)	Lebar (cm)	Luas (cm²)	Keliling (cm)
5	3	15	16
10	3	30	26
5	6	30	22
10	6	60	32

Contoh Kasus dan Soal Cerita

Berikut beberapa contoh kasus yang menunjukkan bagaimana rumus luas dan keliling digunakan dalam situasi nyata:

1. Kasus 1: Diketahui luas taman berbentuk persegi panjang adalah 100 m² dan panjangnya 20 m. Berapa keliling taman tersebut? (Jawab: Lebar = 5 m, Keliling = 50 m)
2. Kasus 2: Sebuah bingkai foto memiliki keliling 60 cm dan lebar 10 cm. Berapa luas bingkai foto tersebut? (Jawab: Panjang = 20 cm, Luas = 200 cm²)
3. Kasus 3: Sebuah lapangan sepak bola memiliki luas 7200 m² dan keliling 360 m. Berapa panjang dan lebar lapangan tersebut? (Jawab: Panjang = 90 m, Lebar = 80 m)

Berikut dua contoh soal cerita yang melibatkan perhitungan luas dan keliling:

1. Soal 1: Bu Ani ingin membuat kebun bunga berbentuk persegi panjang dengan luas 48 m². Jika panjang kebun 8 m, berapa meter keliling kebun tersebut?
2. Soal 2: Pak Budi ingin memasang keramik pada lantai kamar mandi yang berbentuk persegi panjang dengan ukuran 2,5 meter x 1,5 meter. Jika harga keramik Rp 50.000 per meter persegi, berapa biaya yang dibutuhkan Pak Budi untuk membeli keramik? (Konversi satuan: luas kamar mandi dalam m²)

Skenario Optimasi Kandang Ayam

Seorang peternak ingin membuat kandang ayam persegi panjang dengan luas minimal 50 m² dan keliling seminimal mungkin untuk efisiensi penggunaan bahan bangunan. Ukuran panjang dan lebar kandang yang paling efisien dicapai ketika bentuk kandang mendekati bujur sangkar. Dalam kasus ini, panjang dan lebar akan mendekati nilai yang sama, misalnya 7,07 m x 7,07 m, untuk meminimalkan keliling sambil memenuhi persyaratan luas minimal.

Analisis Perubahan Keliling dengan Luas Tetap

Jika luas persegi panjang tetap, perubahan keliling akan mempengaruhi bentuk persegi panjang. Semakin kecil kelilingnya, bentuk persegi panjang akan semakin mendekati bujur sangkar. Sebaliknya, semakin besar kelilingnya, persegi panjang akan semakin memanjang dan menyempit.

Interpretasi Perubahan Luas dengan Keliling Tetap

Jika keliling persegi panjang tetap, perubahan luas akan mempengaruhi bentuk persegi panjang. Semakin besar luasnya, bentuk persegi panjang akan semakin mendekati bujur sangkar. Sebaliknya, semakin kecil luasnya, persegi panjang akan semakin memanjang dan menyempit.

Menentukan Panjang atau Lebar Persegi Panjang

Nah, setelah kita paham rumus luas persegi panjang, sekarang saatnya naik level! Kadang, kita nggak selalu dikasih tahu semua ukuran sisi persegi panjang. Misalnya, kita cuma tahu luasnya dan salah satu sisinya. Tenang, kita tetap bisa nemuin panjang atau lebar yang hilang itu kok! Caranya? Simak penjelasan berikut ini, dijamin anti ribet!

Menentukan panjang atau lebar persegi panjang jika diketahui luas dan salah satu sisinya sebenarnya gampang banget. Kita tinggal sedikit ‘bermain’ dengan rumus luas persegi panjang (Luas = panjang x lebar). Dengan memanipulasi rumus ini, kita bisa cari nilai yang belum diketahui.

Menentukan Panjang atau Lebar Persegi Panjang

Untuk menentukan panjang atau lebar persegi panjang jika luas dan salah satu sisi diketahui, kita bisa menggunakan rumus luas persegi panjang dan melakukan sedikit manipulasi aljabar. Ingat rumusnya: Luas = panjang x lebar. Jika luas dan panjang diketahui, maka lebar = Luas / panjang. Sebaliknya, jika luas dan lebar diketahui, maka panjang = Luas / lebar.

Contoh Soal dan Penyelesaian

Biar lebih jelas, yuk kita lihat beberapa contoh soal dan penyelesaiannya. Contoh-contoh ini akan memperjelas bagaimana kita menerapkan rumus tersebut dalam berbagai situasi.

1. Sebuah persegi panjang memiliki luas 60 cm² dan panjang 10 cm. Berapakah lebarnya?
2. Sebuah kebun berbentuk persegi panjang memiliki luas 100 m² dan lebar 5 m. Berapa panjang kebun tersebut?
3. Sebuah kertas berbentuk persegi panjang memiliki luas 24 cm² dan lebar 4 cm. Tentukan panjang kertas tersebut.

Penyelesaian:

1. Lebar = Luas / panjang = 60 cm² / 10 cm = 6 cm
2. Panjang = Luas / lebar = 100 m² / 5 m = 20 m
3. Panjang = Luas / lebar = 24 cm² / 4 cm = 6 cm

Diagram Alir Menentukan Panjang atau Lebar Persegi Panjang

Untuk memudahkan pemahaman, berikut diagram alir langkah-langkah menentukan panjang atau lebar persegi panjang:

1. Tentukan nilai yang diketahui (luas dan salah satu sisi).
2. Tuliskan rumus luas persegi panjang: Luas = panjang x lebar.
3. Susun ulang rumus untuk mencari sisi yang belum diketahui (panjang atau lebar).
4. Substitusikan nilai yang diketahui ke dalam rumus.
5. Hitung dan temukan nilai sisi yang belum diketahui.

Contoh Soal Cerita

Sekarang, mari kita coba soal cerita yang sedikit lebih menantang. Soal cerita ini akan menguji pemahaman kita dalam menerapkan rumus luas persegi panjang dalam konteks yang lebih nyata.

Bu Ani memiliki sebidang tanah berbentuk persegi panjang. Luas tanah tersebut adalah 120 m². Jika panjang tanah tersebut 15 m, berapa lebar tanah Bu Ani?

Langkah-langkah Penyelesaian Soal Cerita

Untuk menyelesaikan soal cerita di atas, ikuti langkah-langkah berikut:

1. Identifikasi informasi yang diketahui: Luas = 120 m², panjang = 15 m.
2. Tentukan besaran yang ingin dicari: lebar.
3. Gunakan rumus luas persegi panjang: Luas = panjang x lebar.
4. Ubah rumus agar lebar menjadi subjek: lebar = Luas / panjang.
5. Substitusikan nilai yang diketahui ke dalam rumus: lebar = 120 m² / 15 m.
6. Hitung hasilnya: lebar = 8 m.

Penerapan Rumus Persegi Panjang dalam Kehidupan Sehari-hari

Siapa sangka, rumus sederhana luas dan keliling persegi panjang—yaitu Luas = panjang x lebar dan Keliling = 2 x (panjang + lebar)—sebenarnya punya peran penting dalam kehidupan kita sehari-hari? Dari hal-hal kecil hingga proyek besar, rumus ini selalu hadir dan membantu kita menyelesaikan berbagai masalah. Yuk, kita telusuri bagaimana rumus ini diterapkan di berbagai bidang!

Contoh Penerapan Rumus Persegi Panjang dalam Berbagai Konteks

Berikut beberapa contoh unik dan spesifik penerapan rumus luas dan keliling persegi panjang, di luar contoh-contoh umum yang sudah sering kita dengar. Kita akan melihat bagaimana rumus ini berperan dalam berbagai sektor, dari desain rumah hingga pertanian.

Contoh Penerapan	Rumus yang Digunakan	Data (dengan Satuan)	Hasil (dengan Satuan)
Membuat Kanvas Lukis Ukuran Besar	Luas = p x l	p = 200 cm, l = 150 cm	Luas = 30.000 cm²
Perencanaan Bedengan Tanaman Hidroponik	Luas = p x l; Keliling = 2(p+l)	p = 1,5 m, l = 5 m	Luas = 7,5 m², Keliling = 13 m
Desain Cetakan Kue Tart Persegi Panjang	Luas = p x l	p = 30 cm, l = 40 cm	Luas = 1200 cm²
Perhitungan Material untuk Pembuatan Rak di Gudang	Luas = p x l; Volume = p x l x t	p = 2 m, l = 1 m, t = 1,5 m	Luas permukaan = 9 m², Volume = 3 m³
Menghitung Kebutuhan Ubin untuk Lantai Garasi	Luas = p x l	p = 5 m, l = 6 m, ukuran ubin = 0,5 m x 0,5 m	Jumlah ubin = 120 buah

Perhitungan Material di Bidang Arsitektur dan Desain Interior

Bayangkan kamu sedang mendesain sebuah ruang keluarga dengan ukuran 4 meter x 5 meter. Untuk menghitung kebutuhan ubin, kita perlu menghitung luas lantai: Luas = 4 m x 5 m = 20 m². Jika satu kotak ubin berukuran 0,5 m x 0,5 m (luas 0,25 m²), maka dibutuhkan 20 m² / 0,25 m² = 80 kotak ubin. Dengan harga ubin Rp 50.000 per kotak, total biaya ubin adalah 80 kotak x Rp 50.000/kotak = Rp 4.000.000. Perhitungan serupa bisa dilakukan untuk cat dinding, karpet, dan material lainnya.

Aplikasi Rumus Persegi Panjang dalam Pertanian

Misalnya, kita ingin menanam bibit cabai di lahan seluas 100 m². Dengan jarak tanam 50 cm x 50 cm (0,25 m² per tanaman), maka jumlah tanaman yang bisa ditanam adalah 100 m² / 0,25 m² = 400 tanaman. Perhitungan ini membantu petani merencanakan penanaman dan memperkirakan hasil panen.

Optimasi Penggunaan Ruang di Gudang Penyimpanan

Sebuah gudang dengan luas lantai 100 m² dan tinggi 3 meter ingin memaksimalkan kapasitas penyimpanan. Dengan bentuk persegi panjang, kita bisa mengeksplorasi berbagai konfigurasi panjang dan lebar untuk memaksimalkan volume (Volume = panjang x lebar x tinggi). Misalnya, jika kita memilih panjang 10 m dan lebar 10 m, volume gudang adalah 300 m³. Namun, konfigurasi lain mungkin lebih efisien tergantung pada bentuk dan ukuran barang yang disimpan.

Kelebihan dan Kekurangan Rumus Persegi Panjang

Rumus persegi panjang sangat praktis dan mudah diterapkan untuk menghitung luas dan keliling bidang datar berbentuk persegi panjang. Namun, rumus ini kurang tepat digunakan untuk menghitung luas dan keliling bidang yang tidak beraturan, seperti lahan pertanian yang bentuknya tidak sepenuhnya persegi panjang. Dalam kasus seperti ini, dibutuhkan metode perhitungan yang lebih kompleks.

Soal-Soal Latihan dan Pembahasan Perhitungan Luas dan Keliling Persegi Panjang

Nah, setelah memahami rumus luas dan keliling persegi panjang, saatnya kita uji kemampuanmu! Berikut beberapa soal latihan yang akan mengasah pemahamanmu. Soal-soal ini bervariasi tingkat kesulitannya, mulai dari yang mudah hingga yang menantang. Siap-siap beradu otak, ya!

Jangan lupa, kunci sukses mengerjakan soal matematika adalah teliti dan memahami konsepnya. Pahami setiap langkah penyelesaian, bukan hanya menghafal rumus. Jika masih ada yang bingung, jangan ragu untuk membaca kembali materi sebelumnya.

Soal Latihan dan Kunci Jawaban

No.	Soal	Kunci Jawaban
1	Hitunglah luas persegi panjang dengan panjang 5 cm dan lebar 3 cm!	15
2	Sebuah persegi panjang memiliki panjang 7,5 m dan lebar 4,2 m. Berapakah keliling persegi panjang tersebut?	23,4
3	Sebuah taman berbentuk persegi panjang akan ditanami rumput. Panjang taman tersebut 12 meter dan lebarnya 8 meter. Berapakah luas dan keliling taman tersebut?	96, 40
4	Sebuah lantai berbentuk persegi panjang memiliki panjang 250 cm dan lebar 150 cm. Berapakah luas lantai tersebut dalam meter persegi (m2)?	3,75
5	Keliling sebuah persegi panjang adalah 28 cm. Jika panjangnya 10 cm, berapakah luas persegi panjang tersebut?	24

Pembahasan Soal, Rumus tinggi persegi panjang

Soal 1

> Langkah 1: Gunakan rumus luas persegi panjang: Luas = panjang x lebar.
>
> Langkah 2: Substitusikan nilai panjang (5 cm) dan lebar (3 cm) ke dalam rumus: Luas = 5 cm x 3 cm = 15 cm².
>
> Langkah 3: Jadi, luas persegi panjang tersebut adalah 15 cm².

Soal 2

> Langkah 1: Gunakan rumus keliling persegi panjang: Keliling = 2 x (panjang + lebar).
>
> Langkah 2: Substitusikan nilai panjang (7,5 m) dan lebar (4,2 m) ke dalam rumus: Keliling = 2 x (7,5 m + 4,2 m) = 2 x 11,7 m = 23,4 m.
>
> Langkah 3: Jadi, keliling persegi panjang tersebut adalah 23,4 m.

Soal 3

> Langkah 1: Hitung luas taman: Luas = panjang x lebar = 12 m x 8 m = 96 m².
>
> Langkah 2: Hitung keliling taman: Keliling = 2 x (panjang + lebar) = 2 x (12 m + 8 m) = 2 x 20 m = 40 m.
>
> Langkah 3: Jadi, luas taman adalah 96 m² dan kelilingnya 40 m.

Soal 4

> Langkah 1: Ubah satuan panjang dan lebar dari cm ke m: Panjang = 250 cm = 2,5 m; Lebar = 150 cm = 1,5 m.
>
> Langkah 2: Hitung luas lantai: Luas = panjang x lebar = 2,5 m x 1,5 m = 3,75 m².
>
> Langkah 3: Jadi, luas lantai tersebut adalah 3,75 m².

Soal 5

> Langkah 1: Gunakan rumus keliling persegi panjang: Keliling = 2 x (panjang + lebar). Kita tahu kelilingnya 28 cm dan panjangnya 10 cm.
>
> Langkah 2: Cari lebar: 28 cm = 2 x (10 cm + lebar). Maka, 14 cm = 10 cm + lebar, sehingga lebar = 4 cm.
>
> Langkah 3: Hitung luas: Luas = panjang x lebar = 10 cm x 4 cm = 40 cm².
>
> Langkah 4: Jadi, luas persegi panjang tersebut adalah 40 cm².

Persegi Panjang dan Geometri Lanjutan

Persegi panjang, bangun datar yang familiar dengan sisi-sisi berhadapan sejajar dan sama panjang, ternyata punya peran penting dalam geometri yang lebih kompleks. Lebih dari sekadar bangun dasar, persegi panjang menjadi kunci untuk memahami konsep-konsep geometri lanjutan, membuka pintu menuju dunia rumus dan teorema yang lebih menantang. Yuk, kita telusuri bagaimana persegi panjang berperan dalam geometri tingkat lanjut!

Hubungan Persegi Panjang dengan Bangun Datar Lainnya

Persegi panjang memiliki hubungan erat dengan berbagai bangun datar lainnya. Ia bisa dianggap sebagai kasus khusus dari jajar genjang (jajar genjang dengan sudut siku-siku), belah ketupat (belah ketupat dengan sudut siku-siku), dan bahkan layang-layang (layang-layang dengan dua pasang sisi yang sama panjang dan membentuk sudut siku-siku). Memahami sifat-sifat persegi panjang membantu kita memahami sifat-sifat bangun datar yang lebih umum. Misalnya, rumus luas persegi panjang (panjang x lebar) menjadi dasar untuk menghitung luas bangun datar lain yang bisa dibagi menjadi beberapa persegi panjang.

Penerapan Persegi Panjang dalam Geometri Lanjutan

Konsep persegi panjang tak berhenti di geometri dasar. Dalam geometri analitik, misalnya, kita bisa merepresentasikan persegi panjang sebagai himpunan titik-titik pada bidang kartesian yang dibatasi oleh persamaan garis. Penggunaan koordinat kartesian memungkinkan analisis yang lebih presisi terhadap posisi, ukuran, dan hubungan antara persegi panjang dan bangun datar lainnya. Bayangkan bagaimana kita bisa menghitung jarak antar titik sudut persegi panjang atau menentukan persamaan garis yang melalui sisi-sisinya.

Persegi Panjang dan Teorema Pythagoras

Teorema Pythagoras, yang menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat kedua sisi lainnya, memiliki hubungan yang kuat dengan persegi panjang. Bayangkan sebuah segitiga siku-siku. Jika kita membangun persegi pada setiap sisi segitiga tersebut, maka luas persegi yang dibangun pada sisi miring sama dengan jumlah luas persegi yang dibangun pada kedua sisi lainnya. Ini adalah visualisasi geometri dari Teorema Pythagoras, dan persegi panjang berperan sebagai elemen kunci dalam visualisasi ini.

Konsep Geometri Lanjutan yang Melibatkan Persegi Panjang

Banyak konsep geometri lanjutan melibatkan persegi panjang. Contohnya, dalam kalkulus integral, persegi panjang digunakan untuk mendekati luas daerah di bawah kurva. Metode Riemann, misalnya, menggunakan pendekatan ini. Selain itu, dalam geometri dimensi tinggi, konsep persegi panjang diekstensikan menjadi hiper-persegi panjang, yang merupakan bangun ruang dengan lebih dari tiga dimensi. Konsep ini penting dalam berbagai bidang, termasuk pemodelan data dan analisis statistik.

Luas Permukaan dan Volume Bangun Ruang Berkaitan dengan Persegi Panjang

Persegi panjang juga merupakan dasar untuk menghitung luas permukaan dan volume berbagai bangun ruang. Kubus, misalnya, terdiri dari enam persegi panjang yang identik. Balok juga terdiri dari enam persegi panjang (meski tidak selalu identik). Dengan memahami rumus luas dan keliling persegi panjang, kita dapat dengan mudah menghitung luas permukaan dan volume kubus dan balok. Bahkan untuk bangun ruang yang lebih kompleks, konsep persegi panjang sering digunakan sebagai dasar perhitungan.

Rumus Diagonal Persegi Panjang

Persegi panjang, bangun datar yang akrab kita temui sehari-hari, ternyata menyimpan rahasia menarik di balik kesederhanaannya. Salah satu rahasia tersebut adalah rumus diagonalnya. Mungkin kamu pernah melihat diagonal persegi panjang, garis yang menghubungkan dua sudut yang berseberangan. Nah, ternyata panjang diagonal ini bisa dihitung dengan rumus yang sederhana dan elegan. Siap-siap otakmu akan sedikit tertantang, tapi dijamin seru!

Menghitung Panjang Diagonal Persegi Panjang

Rumus untuk menghitung panjang diagonal (d) sebuah persegi panjang dengan panjang (p) dan lebar (l) adalah:

d = √(p² + l²)

Rumus ini berasal dari teorema Pythagoras, yang menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat kedua sisi lainnya. Bayangkan persegi panjangmu dibagi menjadi dua segitiga siku-siku oleh diagonalnya – voila! Teorema Pythagoras langsung bisa diaplikasikan.

Contoh Perhitungan Panjang Diagonal

Yuk, kita coba beberapa contoh. Misalnya, kita punya persegi panjang dengan panjang 6 cm dan lebar 8 cm. Maka, panjang diagonalnya adalah:

d = √(6² + 8²) = √(36 + 64) = √100 = 10 cm

Contoh lainnya: persegi panjang dengan panjang 5 cm dan lebar 12 cm. Coba hitung sendiri, ya! Jawabannya adalah 13 cm. Semakin besar panjang dan lebar, semakin panjang pula diagonalnya. Gampang, kan?

Ilustrasi Persegi Panjang dan Diagonalnya

Bayangkan sebuah persegi panjang ABCD, dengan A di pojok kiri bawah, B di pojok kanan bawah, C di pojok kanan atas, dan D di pojok kiri atas. Diagonal AC menghubungkan titik A dan C. Jika panjang AB (panjang persegi panjang) adalah 6 cm dan BC (lebar persegi panjang) adalah 8 cm, maka panjang diagonal AC bisa dihitung menggunakan rumus di atas, hasilnya 10 cm. Sama seperti contoh sebelumnya, segitiga ABC membentuk segitiga siku-siku dengan sisi miring AC (diagonal).

Perbandingan Panjang Diagonal dengan Panjang dan Lebar

Perhatikan bahwa panjang diagonal selalu lebih panjang daripada panjang dan lebar persegi panjang. Ini karena diagonal merupakan sisi miring segitiga siku-siku yang dibentuk oleh panjang dan lebar. Sebagai contoh, pada persegi panjang dengan panjang 6 cm dan lebar 8 cm, diagonalnya 10 cm – lebih panjang dari 6 cm dan 8 cm.

Penggunaan Rumus Diagonal dalam Geometri

Rumus diagonal persegi panjang bukan cuma sekedar rumus. Ia punya peran penting dalam berbagai permasalahan geometri. Misalnya, dalam menghitung luas permukaan bangun ruang tertentu yang melibatkan persegi panjang, atau dalam menentukan jarak terpendek antara dua titik yang terletak pada sisi-sisi yang berlawanan dari persegi panjang. Rumus ini juga jadi fondasi untuk memahami konsep-konsep geometri yang lebih kompleks.

Persegi Panjang dan Sistem Koordinat

Siapa sangka, bangun datar sederhana seperti persegi panjang ternyata punya hubungan erat dengan sistem koordinat Kartesius! Bayangkan, kita bisa menggambarkan dan menganalisis persegi panjang dengan tepat menggunakan koordinat titik-titik sudutnya. Kemampuan ini membuka jalan untuk berbagai perhitungan geometri yang lebih canggih. Yuk, kita eksplorasi lebih dalam!

Representasi Persegi Panjang dalam Sistem Koordinat Kartesius

Dalam sistem koordinat Kartesius, kita bisa merepresentasikan persegi panjang dengan menentukan koordinat titik-titik sudutnya. Setiap titik sudut memiliki pasangan koordinat (x, y) yang unik. Dengan mengetahui koordinat empat titik sudut ini, kita bisa menggambarkan bentuk dan ukuran persegi panjang secara presisi. Misalnya, persegi panjang ABCD dengan titik A(1,2), B(5,2), C(5,4), dan D(1,4).

Contoh Soal Koordinat Titik Sudut Persegi Panjang

Mari kita coba contoh soal. Misalkan ada persegi panjang EFGH dengan titik E(2,1), F(8,1), dan G(8,6). Tentukan koordinat titik H dan hitung luas persegi panjang tersebut. Dengan memahami sifat persegi panjang, kita tahu bahwa koordinat H adalah (2,6) karena sisi-sisi persegi panjang sejajar dengan sumbu x dan y. Panjang sisi EF adalah 8-2 = 6 satuan dan panjang sisi FG adalah 6-1 = 5 satuan. Luas persegi panjang adalah panjang x lebar = 6 x 5 = 30 satuan luas.

Ilustrasi Persegi Panjang pada Sistem Koordinat

Bayangkan sebuah bidang koordinat Kartesius. Gambarlah sumbu X dan sumbu Y yang saling tegak lurus. Kemudian, plot titik-titik sudut persegi panjang sesuai koordinatnya. Misalnya, untuk persegi panjang dengan titik sudut A(1,1), B(4,1), C(4,3), dan D(1,3), titik A berada satu satuan ke kanan dan satu satuan ke atas dari titik origin (0,0). Titik B empat satuan ke kanan dan satu satuan ke atas. Titik C empat satuan ke kanan dan tiga satuan ke atas. Titik D satu satuan ke kanan dan tiga satuan ke atas. Hubungkan keempat titik tersebut dan Anda akan mendapatkan gambar persegi panjang yang rapi pada sistem koordinat.

Perhitungan Luas dan Keliling Persegi Panjang Berdasarkan Koordinat

Menghitung luas dan keliling persegi panjang dari koordinat titik sudutnya cukup mudah. Kita bisa menggunakan rumus jarak antara dua titik untuk mencari panjang sisi-sisinya. Misalnya, untuk persegi panjang dengan titik sudut (x1, y1), (x2, y1), (x2, y2), dan (x1, y2), panjang sisi pertama adalah |x2 – x1| dan panjang sisi kedua adalah |y2 – y1|. Luas = |x2 – x1| * |y2 – y1|, sedangkan keliling = 2 * (|x2 – x1| + |y2 – y1|).

Hubungan Koordinat Titik Sudut dan Sifat Persegi Panjang

Koordinat titik sudut persegi panjang mencerminkan sifat-sifatnya. Sisi-sisi yang berhadapan memiliki panjang yang sama dan sejajar dengan sumbu koordinat (jika sisi-sisi sejajar dengan sumbu koordinat). Sudut-sudutnya membentuk sudut siku-siku (90 derajat). Dengan menganalisis koordinat, kita bisa memverifikasi apakah bangun datar yang dibentuk memang benar-benar persegi panjang atau bukan.

Mencari Luas Persegi Panjang dengan Informasi Tidak Langsung: Rumus Tinggi Persegi Panjang

Gak cuma langsung dikasih panjang dan lebar, nyari luas persegi panjang bisa lebih menantang, lho! Kadang kita perlu sedikit detektif untuk menemukan informasi yang tersembunyi di balik soal-soal yang unik. Artikel ini bakal ngebantu kamu menguasai trik-trik jitu dalam mencari luas persegi panjang meskipun informasinya nggak langsung diberikan secara gamblang.

Kita akan bahas berbagai kasus, mulai dari soal yang pake persamaan, perbandingan, grafik, sampai soal cerita yang bikin otakmu sedikit berkeringat. Siap-siap asah kemampuan berpikir kritismu, gengs!

Contoh Soal dengan Penalaran Lebih

Berikut tiga contoh soal yang membutuhkan sedikit ekstra usaha untuk menemukan luas persegi panjang. Soal-soal ini bervariasi tingkat kesulitannya, mulai dari yang mudah sampai yang bikin kamu garuk-garuk kepala (tapi tenang, ada solusinya kok!).

1. Soal Mudah: Keliling persegi panjang adalah 24 cm, dan panjangnya 2 cm lebih panjang dari lebarnya. Berapakah luas persegi panjang tersebut?
2. Soal Sedang: Sebuah persegi panjang memiliki diagonal sepanjang 10 cm dan salah satu sisinya sepanjang 6 cm. Tentukan luas persegi panjang tersebut.
3. Soal Sulit: Persegi panjang ABCD memiliki titik A(1,2), B(5,2), C(5,4). Tentukan koordinat titik D dan luas persegi panjang ABCD.

Contoh Soal Cerita dengan Analisis Lebih Dalam

Nah, sekarang kita coba soal cerita yang lebih menantang. Soal-soal ini membutuhkan analisis yang lebih detail untuk menemukan ukuran sisi persegi panjang.

1. Konversi Satuan: Sebuah taman berbentuk persegi panjang memiliki panjang 15 meter dan lebar 800 cm. Berapa luas taman tersebut dalam meter persegi?
2. Perbandingan: Perbandingan panjang dan lebar sebuah persegi panjang adalah 3:2. Jika kelilingnya 50 cm, tentukan luas persegi panjang tersebut.
3. Sistem Persamaan Linear: Jumlah panjang dan lebar sebuah persegi panjang adalah 17 cm, sedangkan selisih panjang dan lebarnya adalah 7 cm. Tentukan luas persegi panjang tersebut.

Langkah-Langkah Menyelesaikan Soal dengan Informasi Tidak Langsung

Supaya nggak bingung, berikut langkah-langkah sistematis untuk menyelesaikan soal-soal yang informasi nya nggak langsung diberikan.

Langkah	Deskripsi	Contoh
1. Memahami Soal	Identifikasi informasi yang diketahui dan yang ditanyakan.	Diketahui: keliling = 20 cm, panjang = 2 kali lebar. Ditanyakan: Luas?
2. Mencari Informasi yang Hilang	Gunakan informasi yang ada untuk mencari informasi yang belum diketahui.	Gunakan rumus keliling untuk mencari lebar.
3. Menghitung Luas	Gunakan rumus luas persegi panjang untuk menghitung luas.	Luas = panjang x lebar
4. Memeriksa Jawaban	Periksa kembali perhitungan dan kesesuaian jawaban dengan konteks soal.	Apakah jawaban masuk akal?

Strategi Penyelesaian Soal yang Efektif dan Efisien

Berikut beberapa tips ampuh untuk menyelesaikan soal-soal luas persegi panjang yang menantang:

• Gambar Diagram: Buat sketsa persegi panjang untuk memvisualisasikan soal.
• Tulis Informasi: Catat semua informasi yang diketahui dan yang ditanyakan secara rapi.
• Pilih Rumus: Tentukan rumus yang tepat dan terapkan dengan benar.
• Periksa Jawaban: Pastikan jawabanmu masuk akal dan sesuai dengan konteks soal.

Contoh Soal dengan Grafik

Bayangkan sebuah grafik yang menunjukkan hubungan antara panjang dan lebar persegi panjang. Misalnya, sumbu X mewakili lebar dan sumbu Y mewakili panjang. Jika grafik menunjukkan hubungan linear, kamu bisa menentukan persamaan garisnya dan menggunakannya untuk mencari luas persegi panjang pada titik tertentu.

Contoh Soal Melibatkan Teorema Pythagoras

Sebuah persegi panjang memiliki diagonal sepanjang 13 cm dan salah satu sisinya sepanjang 5 cm. Gunakan teorema Pythagoras untuk mencari sisi lainnya, lalu hitung luas persegi panjang tersebut.

Menangani Informasi Berlebihan atau Menyesatkan

Kadang, soal bisa memberikan informasi yang nggak perlu atau bahkan menyesatkan. Kunci utamanya adalah fokus pada informasi yang relevan dan abaikan informasi yang nggak dibutuhkan.

Contoh Soal dengan Aljabar

Misalkan panjang persegi panjang adalah x + 3 dan lebarnya x. Jika luasnya 28 cm², tentukan nilai x dan ukuran panjang serta lebar persegi panjang tersebut.

Variasi Soal Persegi Panjang

Persegi panjang, bangun datar yang akrab kita temui sehari-hari, ternyata menyimpan segudang permasalahan matematika yang menarik untuk dipecahkan. Dari yang sederhana hingga yang cukup kompleks, soal-soal tentang persegi panjang bisa melatih kemampuan berpikir logis dan analitis kita. Berikut beberapa variasi soal yang akan menguji kemampuanmu!

Soal-soal berikut ini akan menguji pemahamanmu tentang persegi panjang, mulai dari perhitungan dasar hingga penerapannya dalam konteks yang lebih kompleks. Siap-siap beradu otak, gengs!

Soal Cerita yang Melibatkan Konsep Matematika Lainnya

Soal cerita berikut ini memadukan konsep persegi panjang dengan persamaan linear, sistem persamaan linear, dan persamaan kuadrat. Yuk, kita selami tantangannya!

1. Soal Mudah: Sebuah taman berbentuk persegi panjang memiliki panjang 12 meter dan lebar 8 meter. Berapakah keliling dan luas taman tersebut?
   
   Jawaban: Keliling = 2(panjang + lebar) = 2(12 + 8) = 40 meter. Luas = panjang x lebar = 12 x 8 = 96 meter persegi.
2. Soal Sedang: Panjang sebuah persegi panjang 5 cm lebih panjang dari lebarnya. Jika kelilingnya 38 cm, berapakah panjang dan lebar persegi panjang tersebut?
   
   Jawaban: Misal lebar = x cm, maka panjang = x + 5 cm. Keliling = 2(panjang + lebar) = 2(x + x + 5) = 4x + 10 = 38. Maka 4x = 28, sehingga x = 7 cm (lebar). Panjang = x + 5 = 12 cm.
3. Soal Sulit: Sebuah lahan berbentuk persegi panjang akan dibuat kolam renang dengan luas 100 m². Jika panjang kolam 5 meter lebih panjang dari lebarnya, dan keliling kolam ditambah pagar selebar 1 meter di sekelilingnya, berapakah luas lahan yang dibutuhkan untuk kolam dan pagar tersebut?
   
   Jawaban: Misal lebar kolam = x meter, maka panjang kolam = x + 5 meter. Luas kolam = x(x + 5) = 100. x² + 5x – 100 = 0. Dengan rumus kuadrat, diperoleh x = 8 (lebar). Panjang = 13 meter. Keliling kolam = 2(8 + 13) = 42 meter. Dengan pagar selebar 1 meter, keliling total = 42 + 2(2) = 46 meter. Panjang lahan = 13 + 2 = 15 meter. Lebar lahan = 8 + 2 = 10 meter. Luas lahan = 15 x 10 = 150 meter persegi.

Gabungan Bangun Datar

Berikut ini dua soal yang menggabungkan persegi panjang dengan bangun datar lain. Tantangannya terletak pada bagaimana kita membagi bangun datar tersebut menjadi bagian-bagian yang lebih sederhana untuk dihitung.

1. Soal Sedang: Sebuah halaman berbentuk persegi panjang dengan panjang 15 meter dan lebar 10 meter. Di tengah halaman terdapat kolam renang berbentuk setengah lingkaran dengan diameter 6 meter. Berapakah luas halaman yang tidak terpakai oleh kolam renang?
   
   Jawaban: Luas halaman = 15 x 10 = 150 m². Luas setengah lingkaran = ½ π (6/2)² = 14,14 m². Luas halaman yang tidak terpakai = 150 – 14,14 = 135,86 m².
2. Soal Sulit: Sebuah bangun datar terdiri dari sebuah persegi panjang dengan panjang 12 cm dan lebar 8 cm yang di atasnya terdapat sebuah segitiga siku-siku dengan alas 8 cm dan tinggi 6 cm. Berapakah luas total bangun datar tersebut?
   
   Jawaban: Luas persegi panjang = 12 x 8 = 96 cm². Luas segitiga = ½ x 8 x 6 = 24 cm². Luas total = 96 + 24 = 120 cm².

Skala dan Perbandingan

Soal-soal berikut ini menguji kemampuanmu dalam menerapkan konsep skala dan perbandingan pada persegi panjang. Perhatikan baik-baik skalanya, ya!

1. Soal Sedang: Sebuah persegi panjang memiliki panjang aktual 20 meter dan lebar aktual 15 meter. Gambar persegi panjang tersebut dibuat dengan skala 1:100. Berapakah panjang dan lebar persegi panjang pada gambar, dan berapakah luasnya?
   
   Jawaban: Panjang gambar = 20 m / 100 = 0,2 m = 20 cm. Lebar gambar = 15 m / 100 = 0,15 m = 15 cm. Luas gambar = 20 cm x 15 cm = 300 cm².
2. Soal Sulit: Sebuah denah rumah dibuat dengan skala 1:500. Pada denah, ruang tamu berbentuk persegi panjang memiliki panjang 4 cm dan lebar 3 cm. Berapakah keliling dan luas ruang tamu sebenarnya?
   
   Jawaban: Panjang sebenarnya = 4 cm x 500 = 2000 cm = 20 meter. Lebar sebenarnya = 3 cm x 500 = 1500 cm = 15 meter. Keliling sebenarnya = 2(20 + 15) = 70 meter. Luas sebenarnya = 20 x 15 = 300 meter persegi.

Soal Menantang

Berikut ini soal-soal yang membutuhkan pemahaman konsep yang lebih mendalam dan kemampuan berpikir kritis. Siap menerima tantangan?

1. Soal Sulit: Sebuah tangga yang panjangnya 10 meter disandarkan pada dinding. Ujung bawah tangga berjarak 6 meter dari dinding. Jika bagian bawah tangga digeser 2 meter mendekati dinding, berapakah tinggi tangga yang mencapai dinding sekarang? (Gunakan teorema Pythagoras)
   
   Jawaban: Awalnya, tinggi tangga = √(10² – 6²) = 8 meter. Setelah digeser, jarak ke dinding = 6 – 2 = 4 meter. Tinggi tangga baru = √(10² – 4²) = √84 ≈ 9,17 meter.
2. Soal Sulit: Sebuah persegi panjang ABCD memiliki diagonal AC yang panjangnya 13 cm. Jika panjang AB = 5 cm, tentukan luas persegi panjang ABCD dan panjang sisi BC.
   
   Jawaban: Dengan teorema Pythagoras pada segitiga ABC, BC² = AC² – AB² = 13² – 5² = 144. Maka BC = 12 cm. Luas persegi panjang = AB x BC = 5 x 12 = 60 cm².

Analisis dan Pemecahan Masalah

Soal-soal ini membutuhkan kemampuan analisis dan penalaran yang tajam untuk menemukan solusi. Perhatikan baik-baik informasi yang diberikan!

1. Soal Sedang: Sebuah bingkai foto berbentuk persegi panjang memiliki keliling 60 cm. Jika lebar bingkai 5 cm lebih pendek dari panjangnya, berapakah luas bingkai foto tersebut?
   
   Jawaban: Misal panjang = x cm, lebar = x – 5 cm. Keliling = 2(x + x – 5) = 4x – 10 = 60. Maka 4x = 70, x = 17,5 cm (panjang). Lebar = 12,5 cm. Luas = 17,5 x 12,5 = 218,75 cm².
2. Soal Sulit: Sebuah taman berbentuk persegi panjang memiliki luas 200 m². Jika panjang taman 10 meter lebih panjang dari lebarnya, dan biaya pembuatan pagar sekeliling taman adalah Rp 50.000 per meter, berapakah total biaya pembuatan pagar tersebut?
   
   Jawaban: Misal lebar = x meter, panjang = x + 10 meter. Luas = x(x + 10) = 200. x² + 10x – 200 = 0. Dengan rumus kuadrat, diperoleh x ≈ 10 meter (lebar). Panjang ≈ 20 meter. Keliling = 2(10 + 20) = 60 meter. Total biaya = 60 x 50.000 = Rp 3.000.000.

Aplikasi Rumus Persegi Panjang dalam Pemrograman

Pernah kepikiran nggak, sih, kalau rumus matematika yang sederhana kayak luas dan keliling persegi panjang ternyata punya aplikasi luas banget di dunia pemrograman? Soalnya, konsep dasar perhitungan geometri ini sering banget dipakai dalam berbagai program komputer, dari yang sederhana sampai yang super kompleks. Bayangin aja, bikin game, desain website, atau bahkan aplikasi pengolah gambar, pasti butuh perhitungan-perhitungan geometri, termasuk persegi panjang!

Implementasi Rumus Luas dan Keliling Persegi Panjang dalam Program Sederhana

Penerapan rumus luas dan keliling persegi panjang dalam pemrograman komputer cukup mudah. Kita tinggal menerjemahkan rumus matematika ke dalam kode program. Konsepnya sederhana: program akan meminta input berupa panjang dan lebar persegi panjang, lalu menghitung luas dan kelilingnya berdasarkan rumus yang sudah kita ketahui.

Contoh Kode Program (Python)

Berikut contoh sederhana menggunakan bahasa pemrograman Python:

panjang = float(input("Masukkan panjang persegi panjang: "))
lebar = float(input("Masukkan lebar persegi panjang: "))

luas = panjang * lebar
keliling = 2 * (panjang + lebar)

print("Luas persegi panjang:", luas)
print("Keliling persegi panjang:", keliling)

Kode di atas meminta pengguna memasukkan nilai panjang dan lebar, lalu menghitung dan menampilkan luas serta kelilingnya. Mudah banget, kan?

Algoritma Perhitungan Luas dan Keliling Persegi Panjang

Algoritma yang digunakan dalam program di atas sangat simpel. Secara garis besar, algoritmanya adalah:

1. Ambil input panjang dan lebar dari pengguna.
2. Hitung luas dengan rumus: luas = panjang * lebar
3. Hitung keliling dengan rumus: keliling = 2 * (panjang + lebar)
4. Tampilkan hasil perhitungan luas dan keliling.

Variabel dan Fungsi yang Diperlukan

Dalam program tersebut, kita membutuhkan beberapa variabel dan fungsi. Variabel yang digunakan adalah:

• panjang: Menyimpan nilai panjang persegi panjang.
• lebar: Menyimpan nilai lebar persegi panjang.
• luas: Menyimpan hasil perhitungan luas.
• keliling: Menyimpan hasil perhitungan keliling.

Fungsi yang digunakan adalah fungsi input() untuk mengambil input dari pengguna dan fungsi print() untuk menampilkan output ke layar. Selain itu, operasi matematika dasar seperti perkalian dan penjumlahan juga digunakan.

Implementasi dan Penggunaan Program

Program ini dapat diimplementasikan dengan berbagai bahasa pemrograman, seperti Python, Java, C++, dan lain sebagainya. Setelah program ditulis dan dijalankan, pengguna cukup memasukkan nilai panjang dan lebar persegi panjang, lalu program akan secara otomatis menghitung dan menampilkan luas serta kelilingnya. Program ini sangat berguna untuk berbagai aplikasi, misalnya dalam program CAD (Computer-Aided Design) untuk menghitung luas area atau dalam game untuk menghitung ukuran objek.

Akhir Kata

Jadi, gimana? Setelah membaca artikel ini, rumus tinggi persegi panjang (dalam konteks bangun ruang) dan perhitungan luas serta kelilingnya nggak seram lagi, kan? Sekarang kamu bisa dengan percaya diri menghitung luas lantai rumah, mendesain taman, atau bahkan merencanakan pembangunan gedung pencakar langit! Ingat, matematika itu asyik dan aplikatif. Selamat berkreasi dengan rumus-rumus geometri!