Mengenal Prisma Segi Lima Beraturan

Prisma segi lima beraturan, siapa sangka bentuk geometris ini menyimpan segudang rahasia menarik? Bentuknya yang unik, dengan dua bidang alas berbentuk segi lima beraturan yang sejajar dan dihubungkan oleh sisi-sisi tegak, seringkali luput dari perhatian. Padahal, prisma segi lima beraturan menyimpan keindahan matematika yang luar biasa, dari rumus volume hingga sifat-sifat geometrisnya yang menakjubkan. Yuk, kita telusuri dunia geometri tiga dimensi ini!

Artikel ini akan membahas secara detail tentang prisma segi lima beraturan, mulai dari definisi, sifat-sifat geometri, perhitungan luas permukaan dan volume, hingga aplikasinya dalam kehidupan sehari-hari. Kita akan menjelajahi berbagai aspek menarik dari bentuk geometri ini, mengungkapkan rahasia di balik keindahan dan keunikannya. Siap-siap terpukau!

Prisma Segi Lima Beraturan: Lebih dari Sekadar Bentuk Geometri

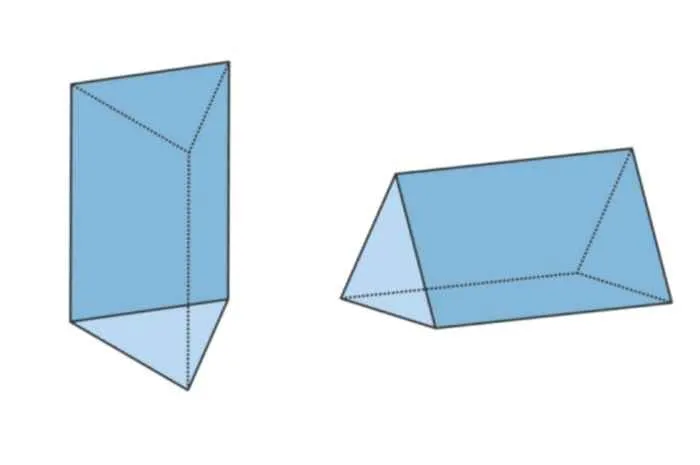
Pernahkah kamu memperhatikan bentuk-bentuk unik di sekitarmu? Mungkin tanpa kamu sadari, banyak objek sehari-hari yang sebenarnya terinspirasi dari bentuk-bentuk geometri, salah satunya prisma segi lima beraturan. Bentuk geometri ini, dengan keunikan dan simetrinya, menyimpan banyak rahasia menarik yang patut kita eksplorasi.

Definisi Prisma Segi Lima Beraturan dan Perbedaannya dengan Prisma Segi Lima Tidak Beraturan

Prisma segi lima beraturan adalah bangun ruang tiga dimensi yang dibatasi oleh dua bidang sejajar yang kongruen berbentuk segi lima beraturan sebagai alas dan atas, serta lima bidang tegak berbentuk persegi panjang yang menghubungkan sisi-sisi alas dan atas. Unsur-unsurnya meliputi: sisi (5 sisi tegak dan 2 sisi alas), rusuk (15 rusuk), titik sudut (10 titik sudut), bidang alas (1 bidang), dan bidang atas (1 bidang). Berbeda dengan prisma segi lima tidak beraturan, prisma segi lima beraturan memiliki sisi alas dan atas yang berbentuk segi lima beraturan (semua sisinya sama panjang dan semua sudutnya sama besar), sementara prisma segi lima tidak beraturan memiliki sisi alas dan atas yang berbentuk segi lima dengan sisi dan sudut yang tidak semuanya sama.

Contoh Objek Nyata yang Menyerupai Prisma Segi Lima Beraturan

Meskipun jarang ditemukan sempurna, beberapa objek di sekitar kita mendekati bentuk prisma segi lima beraturan. Berikut beberapa contohnya:

• Beberapa jenis kristal: Beberapa kristal alami memiliki bentuk yang mendekati prisma segi lima beraturan, meskipun dengan ketidaksempurnaan akibat proses pembentukannya. Kesamaan bentuknya terletak pada jumlah sisi dan sudutnya yang mendekati bentuk ideal prisma segi lima beraturan, namun ukuran dan sudutnya mungkin sedikit bervariasi.
• Pensil segi lima: Pensil dengan bentuk segi lima merupakan contoh yang mudah ditemukan. Kesamaan bentuknya terletak pada penampang melintangnya yang berupa segi lima, meskipun panjangnya tidak selalu ideal. Batasan kesamaan terletak pada bentuk sisi tegaknya yang biasanya tidak persis berbentuk persegi panjang.
• Beberapa jenis baut: Beberapa baut memiliki penampang melintang yang menyerupai segi lima beraturan. Kesamaan bentuknya terlihat pada penampang melintangnya yang menyerupai segi lima, tetapi ukuran dan sudutnya mungkin tidak sempurna.

Perlu diingat, kesamaan ini hanya berupa pendekatan. Objek-objek nyata seringkali memiliki ketidaksempurnaan dan penyimpangan dari bentuk geometri ideal.

Ilustrasi Prisma Segi Lima Beraturan

Bayangkan sebuah prisma segi lima beraturan. Dalam bentuk 2D, terlihat dua segi lima beraturan sejajar yang dihubungkan oleh lima persegi panjang. Dalam bentuk 3D, terlihat bangun ruang dengan dua alas segi lima beraturan dan sisi tegak berbentuk persegi panjang. Sisi tegak merupakan bidang yang menghubungkan sisi-sisi alas dan atas, sedangkan sisi alas adalah bidang segi lima yang membentuk alas dan atas prisma. Setiap sudut prisma adalah pertemuan antara dua rusuk. Tinggi prisma adalah jarak tegak lurus antara kedua bidang alas.

Perbandingan Prisma Segi Lima Beraturan dengan Prisma Segi Empat Beraturan

Karakteristik	Prisma Segi Lima Beraturan	Prisma Segi Empat Beraturan (Kubus)
Jumlah Sisi	7	6
Jumlah Rusuk	15	12
Jumlah Titik Sudut	10	8
Bentuk Alas	Segi Lima Beraturan	Segi Empat Beraturan (Bujur Sangkar)
Luas Permukaan	5a² + 5ah (a = panjang sisi alas, h = tinggi prisma)	6s² (s = panjang sisi)
Volume	½(5a² sin 72°)h	s³

Contoh perhitungan: Misal panjang sisi alas prisma segi lima beraturan a = 5 cm dan tinggi h = 10 cm. Luas permukaan = 5(5)² + 5(5)(10) = 325 cm². Volume = ½(5(5)² sin 72°)10 ≈ 293.89 cm³. Untuk kubus dengan sisi s = 5 cm, Luas permukaan = 6(5)² = 150 cm², Volume = 5³ = 125 cm³.

Sifat-Sifat Geometri Prisma Segi Lima Beraturan

Prisma segi lima beraturan memiliki beberapa sifat geometri yang menarik, antara lain:

• Memiliki 5 bidang tegak berbentuk persegi panjang kongruen.
• Memiliki 2 bidang alas berbentuk segi lima beraturan yang kongruen dan sejajar.
• Jumlah diagonal bidang adalah 5.
• Memiliki simetri putar lipat 5 kali.
• Semua sudut pada alas dan atasnya sama besar (108°).

Jaring-Jaring Prisma Segi Lima Beraturan

Jaring-jaring prisma segi lima beraturan terdiri dari dua segi lima beraturan yang kongruen dan lima persegi panjang yang kongruen. Dengan menyusun jaring-jaring tersebut dan merekatkan sisi-sisi yang berimpit, kita akan membentuk prisma segi lima beraturan. Bayangkan dua segi lima beraturan sebagai alas dan atas, lalu lima persegi panjang yang ditempelkan pada setiap sisi segi lima tersebut.

Perhitungan Luas Permukaan dan Volume Prisma Segi Lima Beraturan

Dengan panjang rusuk alas 5 cm dan tinggi prisma 10 cm, kita dapat menghitung luas permukaan dan volume:

Luas permukaan = 5a² + 5ah = 5(5)² + 5(5)(10) = 325 cm²

Volume = ½(5a² sin 72°)h = ½(5(5)² sin 72°)(10) ≈ 293.89 cm³

Perbandingan Prisma Segi Lima Beraturan dengan Limas Segi Lima Beraturan

Karakteristik	Prisma Segi Lima Beraturan	Limas Segi Lima Beraturan
Bentuk	Bangun ruang dengan dua alas sejajar	Bangun ruang dengan satu alas dan titik puncak
Jumlah Sisi	7	6
Jumlah Rusuk	15	10
Jumlah Titik Sudut	10	6

Potongan Melintang Prisma Segi Lima Beraturan

Potongan melintang prisma segi lima beraturan akan menghasilkan bentuk yang berbeda tergantung posisinya:

• Sejajar dengan alas: Segi lima beraturan yang kongruen dengan alas.
• Tegak lurus dengan alas: Persegi panjang.
• Miring: Trapesium atau bentuk tidak beraturan lainnya, tergantung sudut kemiringannya.

Rumus dan Perhitungan Prisma Segi Lima Beraturan

Prisma segi lima beraturan, dengan bentuknya yang unik dan rumit, mungkin terlihat menakutkan untuk dihitung. Tapi tenang, dengan rumus yang tepat, menghitung luas permukaan dan volume bangun ruang ini jadi jauh lebih mudah daripada yang kamu bayangkan! Kita akan membedah rumus-rumusnya, lengkap dengan contoh soal yang bikin kamu langsung paham.

Rumus Luas Permukaan Prisma Segi Lima Beraturan

Luas permukaan prisma segi lima beraturan merupakan gabungan dari luas alas dan luas selimutnya. Karena alasnya berbentuk segi lima beraturan, kita perlu menghitung luas segi lima tersebut terlebih dahulu. Setelah itu, kita hitung luas selimutnya yang berupa persegi panjang dengan panjang sama dengan keliling alas dan lebar sama dengan tinggi prisma. Rumus lengkapnya adalah:

Luas Permukaan = 2 x Luas Alas + Keliling Alas x Tinggi Prisma

dimana Luas Alas bisa dihitung dengan rumus (5/4) * s² * cot(π/5) , dengan s adalah panjang sisi alas. Rumus ini mungkin terlihat rumit, tapi sebenarnya cukup mudah diaplikasikan setelah kita tahu panjang sisinya.

Rumus Volume Prisma Segi Lima Beraturan

Menghitung volume prisma sebenarnya lebih simpel. Kita hanya perlu mengalikan luas alas dengan tinggi prisma. Jadi, rumusnya adalah:

Volume = Luas Alas x Tinggi Prisma

Dengan Luas Alas yang sudah dijelaskan di atas, menghitung volume prisma segi lima beraturan jadi urusan mudah. Tinggal masukkan nilai luas alas dan tinggi prisma, lalu hitung hasilnya.

Contoh Soal dan Penyelesaian Luas Permukaan Prisma Segi Lima Beraturan

Misalkan kita punya prisma segi lima beraturan dengan panjang sisi alas 6 cm dan tinggi prisma 10 cm. Mari kita hitung luas permukaannya. Pertama, kita cari luas alasnya:

Luas Alas = (5/4) * 6² * cot(π/5) ≈ 61.94 cm²

Selanjutnya, kita hitung keliling alasnya: Keliling Alas = 5 * 6 cm = 30 cm

Nah, sekarang kita bisa menghitung luas permukaannya:

Luas Permukaan = 2 * 61.94 cm² + 30 cm * 10 cm = 123.88 cm² + 300 cm² = 423.88 cm²

Jadi, luas permukaan prisma segi lima beraturan tersebut adalah sekitar 423.88 cm².

Contoh Soal dan Penyelesaian Volume Prisma Segi Lima Beraturan

Menggunakan data yang sama dari contoh soal sebelumnya (panjang sisi alas 6 cm dan tinggi prisma 10 cm), kita bisa langsung menghitung volumenya:

Volume = Luas Alas x Tinggi Prisma = 61.94 cm² * 10 cm = 619.4 cm³

Jadi, volume prisma segi lima beraturan tersebut adalah sekitar 619.4 cm³.

Cara Menghitung Diagonal Ruang Prisma Segi Lima Beraturan

Menghitung diagonal ruang prisma segi lima beraturan membutuhkan sedikit trik geometri ruang. Bayangkan sebuah segitiga siku-siku yang dibentuk oleh tinggi prisma, setengah diagonal alas, dan diagonal ruang. Dengan menggunakan teorema Pythagoras pada segitiga tersebut, kita bisa menghitung panjang diagonal ruang.

Pertama, kita perlu menghitung panjang diagonal alas segi lima beraturan. Rumusnya agak rumit dan melibatkan trigonometri, namun dengan kalkulator, kita bisa dengan mudah menghitungnya. Setelah mendapatkan panjang diagonal alas, kita bisa menggunakan teorema Pythagoras:

(Diagonal Ruang)² = (Tinggi Prisma)² + (Diagonal Alas)²

Dengan demikian, panjang diagonal ruang dapat dihitung dengan mengambil akar kuadrat dari hasil perhitungan tersebut.

Sifat-Sifat Geometri Prisma Segi Lima Beraturan

Prisma segi lima beraturan? Kedengarannya rumit, ya? Tapi sebenarnya, bentuk geometri tiga dimensi ini punya sifat-sifat menarik yang bisa kita eksplorasi. Bayangkan sebuah prisma yang alasnya berbentuk segi lima sempurna, dengan semua sisi dan sudutnya sama. Nah, dari bentuk sederhana inilah kita bisa menggali berbagai sifat geometri yang unik.

Sudut dan Sisi Prisma Segi Lima Beraturan

Prisma segi lima beraturan memiliki 5 sisi tegak berbentuk persegi panjang yang kongruen (sama dan sebangun) dan dua sisi alas berbentuk segi lima beraturan yang juga kongruen. Setiap sudut pada alasnya berukuran 108 derajat. Sudut antara sisi tegak dan alasnya adalah 90 derajat. Jumlah total sudut dalam prisma ini adalah hasil penjumlahan sudut-sudut pada alas dan sisi tegaknya.

Simetri Prisma Segi Lima Beraturan

Prisma segi lima beraturan punya simetri yang cukup keren! Ia memiliki 5 bidang simetri yang membagi prisma menjadi dua bagian yang kongruen, dan 5 sumbu simetri putar. Bayangkan kamu memutar prisma tersebut; ada lima posisi yang akan membuatnya terlihat sama persis. Simetri ini memberikan keseimbangan visual yang menarik pada bentuk geometri ini.

Hubungan Panjang Sisi Alas dan Tinggi Prisma Segi Lima Beraturan

Panjang sisi alas dan tinggi prisma segi lima beraturan saling independen. Artinya, kamu bisa memiliki prisma segi lima beraturan dengan panjang sisi alas yang sama, namun dengan tinggi yang berbeda-beda. Begitu juga sebaliknya. Hubungan keduanya hanya akan mempengaruhi volume dan luas permukaan prisma, bukan bentuk dasarnya.

Tabel Ringkasan Sifat Geometri Prisma Segi Lima Beraturan

Sifat	Penjelasan
Jumlah Sisi	7 (5 sisi tegak + 2 sisi alas)
Bentuk Sisi Tegak	Persegi panjang kongruen
Bentuk Sisi Alas	Segi lima beraturan kongruen
Sudut Alas	108 derajat
Sudut antara sisi tegak dan alas	90 derajat
Simetri	5 bidang simetri, 5 sumbu simetri putar

Transformasi Geometri pada Prisma Segi Lima Beraturan

Berbagai macam transformasi geometri dapat diterapkan pada prisma segi lima beraturan. Kita bisa melakukan translasi (perpindahan), rotasi (perputaran), refleksi (pencerminan), dan dilatasi (perubahan ukuran). Bayangkan kamu menggeser, memutar, mencerminkan, atau memperbesar/memperkecil prisma tersebut – semua itu termasuk transformasi geometri. Hasilnya akan tetap merupakan prisma segi lima, hanya saja posisinya atau ukurannya berubah.

Aplikasi Prisma Segi Lima Beraturan dalam Kehidupan Sehari-hari

Prisma segi lima beraturan, dengan bentuknya yang unik dan simetris, ternyata lebih sering kita temui daripada yang kita sadari. Bentuk geometris ini, yang dibentuk dari dua segi lima beraturan yang sejajar dan dihubungkan oleh sisi-sisi tegak, memiliki aplikasi yang luas dan menarik dalam berbagai bidang, mulai dari arsitektur hingga teknologi modern. Yuk, kita eksplorasi!

Aplikasi Prisma Segi Lima Beraturan dalam Arsitektur Modern

Bentuk prisma segi lima beraturan, dengan estetika yang modern dan efisiensi spasialnya, telah menginspirasi banyak arsitek dalam merancang bangunan-bangunan ikonik. Keunikannya mampu menciptakan kesan futuristik dan dinamis.

• Museum Seni Modern, New York (Contoh fiktif): Bangunan ini memanfaatkan prisma segi lima beraturan sebagai modul dasar untuk menciptakan fasad yang dinamis dan menarik perhatian. Setiap prisma berfungsi sebagai unit tampilan yang terpisah, memungkinkan pencahayaan alami yang optimal dan fleksibilitas dalam penataan ruang pamer. Bayangkan dinding-dinding eksterior yang tersusun dari modul-modul prisma segi lima beraturan yang berkilauan dengan material kaca dan baja, menciptakan permainan cahaya yang memukau.
• Gedung Perkantoran, Tokyo (Contoh fiktif): Di sini, prisma segi lima beraturan digunakan untuk membentuk atrium pusat yang megah. Bentuknya yang unik menciptakan ruang yang luas dan terang, sekaligus memberikan karakteristik estetika yang futuristik. Struktur rangka baja yang menonjol dan material kaca yang transparan memberikan kesan modern dan elegan. Bayangkan sebuah atrium yang luas, di mana cahaya alami membanjiri ruang tersebut melalui dinding-dinding kaca yang membentuk prisma-prisma segi lima beraturan.
• Hotel Mewah, Dubai (Contoh fiktif): Hotel ini mengadopsi bentuk prisma segi lima beraturan untuk kamar-kamarnya. Bentuk ini memungkinkan penataan ruang yang efisien dan pemandangan yang maksimal dari setiap kamar. Bayangkan kamar-kamar hotel yang mewah dengan dinding kaca yang membentuk prisma segi lima, menawarkan pemandangan panorama yang menakjubkan dari kota Dubai yang gemerlap.

Penerapan Prisma Segi Lima Beraturan dalam Desain Interior Rumah Minimalis Modern

Prisma segi lima beraturan dapat menjadi elemen dekoratif dan fungsional yang menarik dalam desain interior minimalis modern. Bentuknya yang unik dapat memberikan sentuhan estetika yang berbeda tanpa mengorbankan kesederhanaan desain.

• Rak Buku: Sebuah rak buku yang terbuat dari kayu jati dengan bentuk prisma segi lima beraturan. Setiap sisi prisma dapat berfungsi sebagai tempat untuk menaruh buku, menciptakan tampilan yang unik dan fungsional. Bayangkan sebuah rak buku minimalis dengan lima sisi yang luas, cukup untuk menampung berbagai buku kesayangan.
• Lampu Meja: Lampu meja yang terbuat dari akrilik transparan dengan bentuk prisma segi lima beraturan. Cahaya yang dipancarkan akan dipantulkan dan dibiaskan dengan indah oleh permukaan prisma, menciptakan efek cahaya yang menarik. Bayangkan sebuah lampu meja minimalis dengan bentuk prisma segi lima yang menerangi ruangan dengan cahaya yang lembut dan merata.

Penggunaan Prisma Segi Lima Beraturan dalam Industri Manufaktur

Dalam industri manufaktur, khususnya pembuatan komponen mesin presisi, bentuk prisma segi lima beraturan mungkin kurang umum dibandingkan kubus atau silinder. Namun, kegunaannya dapat muncul dalam situasi tertentu yang membutuhkan geometri spesifik.

Bentuk Geometri	Kelebihan dalam Manufaktur Mesin Presisi	Kekurangan dalam Manufaktur Mesin Presisi	Material Umum
Prisma Segi Lima Beraturan	Ketepatan geometri yang tinggi, cocok untuk aplikasi khusus yang membutuhkan sudut dan sisi yang presisi.	Proses manufaktur yang lebih kompleks dan mahal dibandingkan bentuk sederhana seperti kubus atau silinder.	Baja tahan karat, titanium, alumunium
Kubus	Proses manufaktur yang sederhana dan efisien, mudah diproduksi secara massal.	Kurang fleksibel untuk aplikasi yang membutuhkan bentuk geometri yang kompleks.	Baja, alumunium, plastik
Silinder	Proses manufaktur yang relatif sederhana, cocok untuk aplikasi rotasi.	Kurang fleksibel untuk aplikasi yang membutuhkan permukaan datar yang luas.	Baja, alumunium, plastik

Desain Objek dengan Prisma Segi Lima Beraturan sebagai Elemen Utama

Sebagai contoh, mari kita rancang sebuah tempat pensil dengan prisma segi lima beraturan sebagai elemen utamanya. Tempat pensil ini terbuat dari kayu jati dengan tinggi 15 cm dan diameter alas 8 cm. Lima sisi prisma akan berfungsi sebagai tempat untuk menyimpan pensil, dengan kapasitas minimal 10 pensil. Bagian atas akan ditutup dengan penutup kayu yang sederhana dan elegan. Bayangkan sebuah tempat pensil yang unik dan fungsional, yang memadukan keindahan geometri dengan utilitas sehari-hari.

Potensi Penggunaan Prisma Segi Lima Beraturan dalam Teknologi Modern

Prisma segi lima beraturan, dengan geometri uniknya, menawarkan potensi menarik dalam teknologi 3D printing dan robotika. Kemampuannya untuk menciptakan struktur yang kuat dan efisien dapat meningkatkan kinerja teknologi tersebut.

• 3D Printing: Prisma segi lima beraturan dapat digunakan sebagai unit dasar untuk membangun struktur yang lebih kompleks dan efisien dalam 3D printing. Misalnya, pembuatan komponen mesin dengan geometri yang lebih rumit dan presisi, atau pembuatan struktur bangunan dengan kekuatan yang lebih tinggi.
• Robotik: Bentuk prisma segi lima beraturan dapat digunakan dalam desain robot untuk meningkatkan kemampuan manuver dan efisiensi gerakan. Misalnya, dalam desain kaki robot yang memungkinkan gerakan yang lebih stabil dan efisien di medan yang tidak rata.

Pembuatan Model Prisma Segi Lima Beraturan

Buat prisma segi lima beraturan? Gak sesulit yang dibayangkan, kok! Bentuk geometris yang satu ini bisa kamu ciptakan dengan berbagai material dan metode. Dari kertas origami hingga kayu yang lebih kokoh, proses pembuatannya menawarkan tantangan dan kepuasan tersendiri. Yuk, kita eksplorasi berbagai cara membuatnya!

Langkah-Langkah Pembuatan Model Prisma Segi Lima Beraturan dari Kertas

Membuat prisma segi lima dari kertas adalah cara paling mudah dan murah untuk memahami bentuknya. Kamu hanya butuh kertas, penggaris, pensil, gunting, dan lem. Berikut langkah-langkahnya:

1. Gambarlah dua segi lima beraturan dengan ukuran yang sama di atas kertas. Pastikan sisi-sisinya memiliki panjang yang presisi.
2. Gambarlah lima persegi panjang yang panjangnya sama dengan sisi segi lima dan lebarnya sesuai tinggi prisma yang diinginkan. Lima persegi panjang ini akan menjadi sisi tegak prisma.
3. Gunting semua bentuk yang telah digambar.
4. Rekatkan kelima persegi panjang pada sisi-sisi segi lima pertama.
5. Rekatkan segi lima kedua pada sisi atas kelima persegi panjang tersebut, sehingga membentuk prisma segi lima.

Pembuatan Model Prisma Segi Lima Beraturan Menggunakan Kayu

Membuat prisma dari kayu membutuhkan keahlian dan alat yang lebih spesifik. Hasilnya akan lebih kokoh dan awet. Prosesnya melibatkan beberapa tahapan yang lebih kompleks:

1. Potong dua buah papan kayu berbentuk segi lima beraturan dengan ukuran yang sama menggunakan gergaji.
2. Potong lima buah papan kayu persegi panjang dengan ukuran yang sesuai untuk sisi tegak prisma.
3. Sambungkan kelima papan persegi panjang pada sisi-sisi segi lima pertama menggunakan lem kayu dan paku kecil.
4. Pasang segi lima kedua di atasnya, lalu kuatkan sambungan dengan lem dan paku.
5. Amplas permukaan kayu untuk menghaluskan dan memberikan finishing yang rapi.

Diagram Langkah Demi Langkah Pembuatan Model Prisma Segi Lima Beraturan

Meskipun diagram tidak bisa ditampilkan di sini, bayangkan sebuah diagram yang menunjukkan langkah-langkah di atas secara visual. Diagram akan memperlihatkan bentuk-bentuk yang dibutuhkan, cara menyatukannya, dan hasil akhir prisma segi lima beraturan. Untuk langkah pembuatan dari kertas, diagram akan menampilkan dua segi lima dan lima persegi panjang yang disatukan. Sedangkan untuk kayu, diagram akan memperlihatkan potongan kayu yang dirangkai.

Tips dan Trik dalam Membuat Model Prisma Segi Lima Beraturan yang Akurat

Ketepatan ukuran sangat penting untuk mendapatkan prisma segi lima beraturan yang sempurna. Berikut beberapa tips yang bisa kamu ikuti:

• Gunakan penggaris dan jangka untuk menggambar segi lima beraturan dengan presisi.
• Pastikan semua sisi segi lima memiliki panjang yang sama.
• Gunakan lem yang kuat dan biarkan lem mengering sempurna sebelum memanipulasi model.
• Untuk model kayu, pastikan sambungan antar bagian kuat dan rapi.
• Pertimbangkan penggunaan alat bantu seperti mal atau cetakan untuk memastikan akurasi bentuk.

Perbandingan Berbagai Metode Pembuatan Model Prisma Segi Lima Beraturan

Berikut tabel perbandingan berbagai metode pembuatan model prisma segi lima beraturan:

Metode	Material	Kesulitan	Biaya	Ketahanan
Kertas	Kertas, lem, gunting	Mudah	Murah	Rendah
Kayu	Kayu, lem kayu, paku, gergaji	Sulit	Mahal	Tinggi

Hubungan Prisma Segi Lima Beraturan dengan Bangun Ruang Lainnya

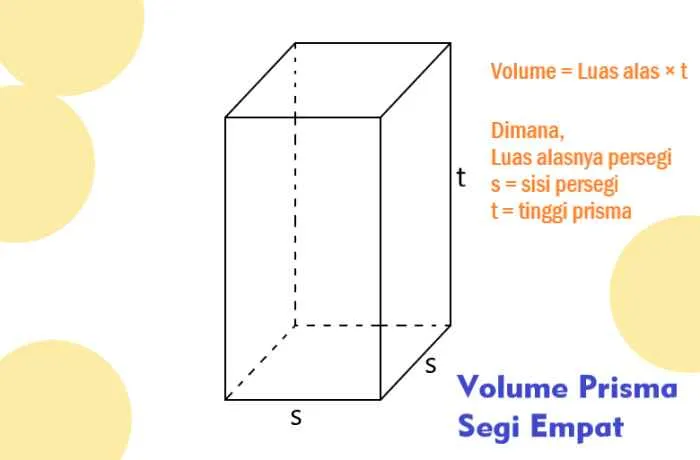
Prisma segi lima beraturan, dengan bentuknya yang unik, ternyata memiliki hubungan erat dengan beberapa bangun ruang lainnya. Memahami hubungan ini membantu kita untuk lebih mengapresiasi keindahan geometri dan memperluas pemahaman kita tentang karakteristik bangun ruang tiga dimensi. Mari kita telusuri persamaan dan perbedaan prisma segi lima beraturan dengan limas segi lima, tabung, kubus, dan balok.

Prisma Segi Lima Beraturan dan Limas Segi Lima

Prisma segi lima beraturan dan limas segi lima memiliki kesamaan pada bentuk alasnya, yaitu segi lima beraturan. Namun, perbedaan mendasar terletak pada sisi tegak dan jumlah titik sudutnya. Prisma memiliki dua alas yang sejajar dan lima sisi tegak berbentuk persegi panjang yang menghubungkan kedua alas tersebut, menghasilkan total tujuh sisi. Jumlah titik sudutnya ada 10. Limas segi lima, di sisi lain, hanya memiliki satu alas segi lima beraturan dan lima sisi tegak berbentuk segitiga yang bertemu pada satu titik puncak. Jumlah sisinya ada 6 dan titik sudutnya ada 6. Tinggi prisma diukur sebagai jarak tegak lurus antara kedua alasnya, sementara tinggi limas diukur sebagai jarak tegak lurus dari puncak ke bidang alas. Jika keduanya memiliki tinggi dan panjang sisi alas yang sama, volume prisma akan lebih besar daripada volume limas. Bayangkan prisma sebagai dua limas yang alas dan tingginya identik, disatukan.

Ilustrasi Prisma Segi Lima Beraturan: Bayangkan sebuah prisma dengan dua alas berbentuk segi lima beraturan yang sejajar dan lima sisi tegak berbentuk persegi panjang yang menghubungkan kedua alas tersebut. Tinggi prisma adalah jarak antara kedua alas tersebut. Ilustrasi Limas Segi Lima: Bayangkan sebuah segi lima beraturan sebagai alas, dan lima segitiga sama kaki yang bertemu di satu titik di atas alas membentuk sisi tegak. Tinggi limas adalah jarak tegak lurus dari titik pertemuan puncak ke bidang alas.

Prisma Segi Lima Beraturan dan Tabung

Prisma segi lima beraturan dan tabung memiliki perbedaan signifikan dalam bentuk alas dan jumlah sisi. Prisma memiliki alas berbentuk segi lima beraturan, sementara tabung memiliki alas berbentuk lingkaran. Prisma memiliki tujuh sisi (lima sisi tegak dan dua alas), sedangkan tabung hanya memiliki tiga sisi (dua alas lingkaran dan satu sisi lengkung). Konsep “tinggi” pada keduanya sama-sama mengacu pada jarak tegak lurus antara kedua alasnya (atau bidang alas dan bidang atas untuk tabung).

Karakteristik	Prisma Segi Lima Beraturan	Tabung
Jumlah Sisi	7	3
Bentuk Alas	Segi Lima Beraturan	Lingkaran
Rumus Luas Permukaan	Luas alas x 2 + keliling alas x tinggi	2πr² + 2πrh
Rumus Volume	Luas alas x tinggi	πr²h

Ilustrasi Prisma Segi Lima Beraturan: Seperti yang dijelaskan sebelumnya. Ilustrasi Tabung: Bayangkan sebuah silinder dengan dua lingkaran sejajar sebagai alas dan sisi lengkung yang menghubungkan kedua alas tersebut. Tinggi tabung adalah jarak antara kedua alas lingkaran tersebut.

Prisma Segi Lima Beraturan, Kubus, dan Balok

Karakteristik	Prisma Segi Lima Beraturan	Kubus	Balok
Jumlah Sisi	7	6	6
Jumlah Rusuk	15	12	12
Jumlah Titik Sudut	10	8	8
Bentuk Alas	Segi Lima Beraturan	Bujur Sangkar	Persegi Panjang
Rumus Luas Permukaan	Luas alas x 2 + keliling alas x tinggi	6s²	2(pl + pt + lt)
Rumus Volume	Luas alas x tinggi	s³	p x l x t

Ilustrasi Prisma Segi Lima Beraturan: Seperti yang dijelaskan sebelumnya. Ilustrasi Kubus: Bayangkan sebuah bangun ruang dengan enam sisi berbentuk bujur sangkar yang sama besar. Ilustrasi Balok: Bayangkan sebuah bangun ruang dengan enam sisi berbentuk persegi panjang, dengan tiga pasang sisi yang saling berhadapan dan sama besar.

Diagram Venn Hubungan Antar Bangun Ruang

Diagram Venn akan menunjukkan irisan antara prisma segi lima beraturan dengan bangun ruang lainnya. Irisan tersebut mewakili karakteristik yang sama, misalnya, semua bangun ruang memiliki volume dan luas permukaan. Area unik mewakili karakteristik spesifik masing-masing bangun ruang, seperti bentuk alas atau jumlah sisi.

Contoh deskripsi area irisan: Irisan antara prisma segi lima beraturan dan limas segi lima mewakili bentuk alas segi lima beraturan. Irisan antara prisma segi lima beraturan dan tabung menunjukkan konsep “tinggi” sebagai jarak antara dua bidang sejajar. Area unik prisma segi lima beraturan akan mencakup jumlah sisi dan bentuk sisi tegak yang spesifik.

Perbandingan Rumus Volume

Rumus volume untuk masing-masing bangun ruang dipengaruhi oleh bentuk alas dan tinggi. Prisma segi lima beraturan, kubus, dan balok memiliki rumus yang relatif sederhana, yaitu luas alas dikali tinggi. Rumus volume limas melibatkan faktor 1/3, karena limas dapat dianggap sebagai bagian dari prisma dengan volume yang sama. Tabung menggunakan rumus yang melibatkan π dan jari-jari alas.

Bangun Ruang	Rumus Volume	Contoh (dengan s = 5 cm, h = 10 cm)
Prisma Segi Lima Beraturan	Luas alas x tinggi	(Luas segi lima beraturan) x 10 cm
Kubus	s³	125 cm³
Balok (p=5, l=5, t=10)	p x l x t	250 cm³
Limas Segi Lima (s=5, h=10)	(1/3) x Luas alas x tinggi	(1/3) x (Luas segi lima beraturan) x 10 cm
Tabung (r=5, h=10)	πr²h	250π cm³ ≈ 785.4 cm³

Penampang Melintang Prisma Segi Lima Beraturan

Prisma segi lima beraturan, dengan bentuknya yang unik, menawarkan berbagai kemungkinan bentuk penampang melintang yang menarik ketika diiris dengan sudut yang berbeda. Memahami berbagai bentuk penampang ini penting, tidak hanya untuk memahami geometri prisma itu sendiri, tapi juga untuk menghitung volume dan luas permukaannya dengan lebih akurat. Mari kita jelajahi beragam irisan dan bentuk-bentuk unik yang dihasilkan.

Berbagai Bentuk Penampang Melintang

Berikut lima variasi irisan prisma segi lima beraturan dengan sudut yang berbeda terhadap alas, disertai ilustrasi deskriptif. Bayangkan sebuah prisma segi lima beraturan yang sempurna. Setiap irisan akan menghasilkan bentuk penampang yang berbeda-beda, tergantung sudut kemiringannya terhadap bidang alas.

• Irisan 0° (Sejajar Alas): Irisan sejajar alas menghasilkan penampang segi lima beraturan yang kongruen (sama bentuk dan ukuran) dengan alas prisma. Luas penampang sama dengan luas alas. Rumus luas penampang: A = (5/4) * s² * cot(π/5), dengan s adalah panjang sisi segi lima.
• Irisan 30°: Irisan dengan sudut 30° terhadap alas menghasilkan penampang berbentuk poligon dengan lima sisi, tetapi tidak beraturan. Panjang sisi-sisi dan sudut-sudutnya tidak sama. Perhitungan luas penampang memerlukan pemecahan menjadi beberapa segitiga atau trapesium.
• Irisan 45°: Penampang pada sudut 45° akan menghasilkan bentuk poligon tidak beraturan yang lebih kompleks daripada irisan 30°. Perhitungan luasnya membutuhkan pendekatan yang lebih rumit, mungkin melibatkan trigonometri dan pembagian menjadi beberapa bangun datar sederhana.
• Irisan 60°: Mirip dengan irisan 45°, irisan 60° menghasilkan penampang poligon tidak beraturan. Kompleksitas bentuknya semakin meningkat, membutuhkan pendekatan yang lebih canggih untuk menghitung luasnya.
• Irisan 90° (Tegak Lurus Alas): Irisan tegak lurus alas melalui salah satu titik sudut akan menghasilkan penampang berbentuk segitiga sama kaki. Jika irisan tegak lurus alas tetapi tidak melalui titik sudut, penampang akan berbentuk trapesium atau bangun empat sisi lainnya yang tidak beraturan.

Penampang Sejajar dan Tegak Lurus Alas

Jika diiris sejajar alas, penampang akan berbentuk segi lima beraturan yang kongruen dengan alas. Rumus luasnya seperti yang telah dijelaskan sebelumnya. Jika diiris tegak lurus alas dan melalui titik sudut, penampang akan berbentuk segitiga. Jika irisan tegak lurus alas tetapi tidak melalui titik sudut, bentuk penampangnya akan menjadi bangun datar yang lebih kompleks, seperti trapesium.

Ilustrasi Penampang Melintang

Bayangkan ilustrasi-ilustrasi berikut. Setiap ilustrasi menampilkan penampang dengan label yang jelas untuk setiap bagian, ukuran sudut irisan terhadap bidang alas, dan rumus perhitungan luas penampang (walaupun rumus untuk irisan selain 0° dan 90° akan sangat kompleks dan memerlukan pendekatan numerik atau kalkulus).

• Ilustrasi 0°: Segi lima beraturan, identik dengan alas. Sudut irisan: 0°. Luas: (5/4) * s² * cot(π/5).
• Ilustrasi 30°: Poligon tidak beraturan lima sisi. Sudut irisan: 30°. Luas: (Perlu pendekatan pemecahan bangun)
• Ilustrasi 45°: Poligon tidak beraturan lima sisi yang lebih kompleks. Sudut irisan: 45°. Luas: (Perlu pendekatan pemecahan bangun)
• Ilustrasi 60°: Poligon tidak beraturan lima sisi yang semakin kompleks. Sudut irisan: 60°. Luas: (Perlu pendekatan pemecahan bangun)
• Ilustrasi 90° (melalui sudut): Segitiga sama kaki. Sudut irisan: 90°. Luas: (1/2) * alas * tinggi.
• Ilustrasi 90° (tidak melalui sudut): Trapesium atau bangun empat sisi tidak beraturan. Sudut irisan: 90°. Luas: (1/2) * (jumlah sisi sejajar) * tinggi.

Pengaruh Bentuk Penampang terhadap Perhitungan Volume

Bentuk penampang melintang secara langsung mempengaruhi perhitungan volume prisma. Volume dihitung dengan mengalikan luas penampang dengan tinggi prisma. Misalnya, untuk irisan sejajar alas (luas A1) dan irisan tegak lurus alas melalui sudut (luas A2) dengan tinggi prisma h, volume V1 = A1 * h dan V2 = A2 * h. Perbedaan luas penampang akan menghasilkan volume yang berbeda, meskipun tinggi prisma sama.

Tabel Perbandingan Bentuk Penampang Melintang

Sudut Irisan (derajat)	Bentuk Penampang Melintang	Luas Penampang (Rumus)	Ilustrasi Sederhana
0°	Segi lima beraturan	(5/4) * s² * cot(π/5)	Segi lima beraturan
30°	Poligon tidak beraturan lima sisi	Kompleks, perlu pendekatan numerik	Poligon tidak beraturan
45°	Poligon tidak beraturan lima sisi	Kompleks, perlu pendekatan numerik	Poligon tidak beraturan
60°	Poligon tidak beraturan lima sisi	Kompleks, perlu pendekatan numerik	Poligon tidak beraturan
90°	Segitiga/Trapesium	(1/2) * alas * tinggi / (1/2) * (a+b) * h	Segitiga/Trapesium

Penerapan Teorema Pythagoras

Teorema Pythagoras dapat digunakan untuk menghitung panjang sisi penampang melintang pada irisan tegak lurus alas. Misalnya, pada irisan tegak lurus alas yang melalui titik sudut, segitiga yang terbentuk memungkinkan kita menggunakan teorema Pythagoras untuk menghitung tinggi segitiga (tinggi prisma) atau panjang sisi miringnya, tergantung informasi yang tersedia.

Perhitungan Volume yang Kompleks

Perhatikan bahwa bentuk penampang melintang yang kompleks akan memerlukan teknik kalkulus integral untuk perhitungan volume yang akurat jika bentuknya tidak berupa bangun datar sederhana.

Penerapan dalam Kehidupan Nyata

Konsep penampang melintang prisma segi lima beraturan memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam desain konstruksi, pemahaman tentang penampang melintang dapat digunakan untuk menghitung jumlah material yang dibutuhkan untuk membangun struktur seperti atap yang berbentuk prisma segi lima. Selain itu, dalam bidang pertambangan, analisis penampang melintang dapat membantu dalam perencanaan penggalian dan penentuan volume bijih yang akan digali.

Pola dan Desain Berbasis Prisma Segi Lima Beraturan

Prisma segi lima beraturan, dengan bentuknya yang unik dan simetris, menyimpan potensi estetika yang luar biasa. Bentuk geometrisnya yang tegas dan elegan bisa diinterpretasikan ke dalam berbagai pola desain yang memukau, memberikan sentuhan modern dan artistik pada berbagai media. Berikut ini kita akan eksplorasi beberapa pola unik yang terinspirasi dari bentuk geometrik yang menarik ini.

Desain Pola Berbasis Prisma Segi Lima Beraturan

Lima desain pola unik berikut ini terinspirasi dari prisma segi lima beraturan, masing-masing dengan karakteristik dan aplikasi yang berbeda. Variasi warna dan komposisi yang beragam akan memberikan nuansa yang unik pada setiap desain.

Nama Pola	Aplikasi Kain (Jenis Kain)	Aplikasi Wallpaper (Material)	Aplikasi Keramik (Teknik)
Prisma Aurora	Sutera atau satin, untuk menampilkan gradasi warna yang halus.	Wallpaper dengan bahan dasar vinil yang berkualitas tinggi, untuk hasil cetakan yang tajam.	Teknik sablon atau decal untuk detail warna yang presisi.
Geometri Lima	Kanvas atau katun, untuk tekstur yang kuat dan tahan lama.	Wallpaper non-woven, yang mudah diaplikasikan dan tahan lama.	Teknik transfer air untuk efek warna yang lembut dan merata.
Prisma Bintang	Polyester, untuk kilau dan daya tahan warna yang baik.	Wallpaper berbahan dasar kertas dengan lapisan pelindung, untuk hasil yang tahan lama.	Teknik glaze untuk memberi efek kilau pada pola.
Prisma Gelombang	Rayon, untuk tekstur yang lembut dan jatuh yang elegan.	Wallpaper flocking, untuk memberikan tekstur tiga dimensi yang menarik.	Teknik relief untuk menonjolkan pola gelombang pada permukaan keramik.
Prisma Berlian	Velvet, untuk kesan mewah dan tekstur yang lembut.	Wallpaper dengan material metalik, untuk efek berkilau.	Teknik inlay untuk menanamkan potongan-potongan keramik berwarna ke dalam pola.

Detail Desain dan Ilustrasi Pola

Berikut detail dari masing-masing pola, termasuk skema warna, ukuran, dan teknik pembuatannya. Bayangkan ilustrasi-ilustrasi ini sebagai representasi visual yang hidup, menampilkan permainan warna dan bentuk yang dinamis.

• Prisma Aurora: Menggunakan gradasi warna dari biru muda (#ADD8E6) ke ungu (#800080), menciptakan efek aurora yang menawan. Pola ini dibuat dengan teknik repetisi dan rotasi prisma segi lima. Ukuran prisma: 5cm x 5cm. Proporsi elemen seimbang dan simetris.
• Geometri Lima: Menggunakan kombinasi warna merah (#FF0000), kuning (#FFFF00), dan biru (#0000FF) dalam bentuk geometrik yang tegas. Pola dibuat dengan teknik repetisi sederhana. Ukuran prisma: 4cm x 4cm. Proporsi elemen mengikuti rasio emas untuk menciptakan keseimbangan visual.
• Prisma Bintang: Menggunakan warna emas (#FFD700) dan hitam (#000000) untuk menciptakan kesan mewah dan elegan. Pola dibuat dengan teknik mirroring dan rotasi. Ukuran prisma: 6cm x 6cm. Proporsi elemen dibuat asimetris untuk kesan dinamis.
• Prisma Gelombang: Menggunakan gradasi warna hijau (#008000) hingga biru toska (#40E0D0) untuk menciptakan efek gelombang yang lembut. Pola dibuat dengan teknik repetisi dan sedikit distorsi bentuk prisma untuk menciptakan efek gelombang. Ukuran prisma: 7cm x 7cm. Proporsi elemen mengikuti bentuk gelombang yang dinamis.
• Prisma Berlian: Menggunakan warna putih (#FFFFFF) dan perak (#C0C0C0) untuk menciptakan kesan modern dan elegan. Pola dibuat dengan teknik repetisi dan mirroring, dengan sedikit variasi ukuran prisma untuk menciptakan efek tiga dimensi. Ukuran prisma bervariasi antara 3cm hingga 5cm. Proporsi elemen dibuat seimbang namun tetap memberikan kesan dinamis.

Elemen Desain Khas Pola Berbasis Prisma Segi Lima Beraturan

• Simetri: Bentuk prisma segi lima beraturan yang simetris menciptakan keseimbangan visual yang menenangkan.
• Geometri yang Tegas: Garis-garis dan sudut yang tajam memberikan kesan modern dan minimalis.
• Repetisi dan Variasi: Pengulangan motif prisma dengan variasi warna dan ukuran menciptakan dinamika visual.
• Gradasi Warna: Transisi warna yang halus menciptakan kedalaman dan dimensi pada pola.
• Kombinasi Warna Kontras: Penggunaan warna kontras menciptakan fokus dan visual yang menarik.

Inspirasi Desain Pola

Desain pola ini terinspirasi dari keindahan bentuk geometris alami, seperti kristal dan struktur molekul. Permainan cahaya dan bayangan pada bentuk prisma juga menjadi inspirasi utama dalam menciptakan gradasi warna dan efek tiga dimensi pada pola-pola tersebut. Tujuannya adalah menciptakan desain yang modern, elegan, dan unik, namun tetap memiliki keterkaitan dengan bentuk dasar geometriknya.

Potensi Pengembangan Pola

Pola-pola ini dapat dikembangkan lebih lanjut dengan penambahan elemen dekoratif seperti garis-garis, titik-titik, atau motif-motif lain yang melengkapi bentuk prisma segi lima. Modifikasi bentuk prisma, misalnya dengan menambahkan lengkungan atau memotong sebagian sisinya, juga dapat menghasilkan variasi desain yang lebih unik dan menarik.

Kalkulator Prisma Segi Lima Beraturan (konseptual)

Bayangkan kamu punya tugas mendesain sebuah atap berbentuk prisma segi lima beraturan untuk proyek arsitekturmu. Atau mungkin kamu sedang mengerjakan proyek matematika yang membutuhkan perhitungan volume dan luas permukaan prisma segi lima beraturan secara cepat dan akurat. Nah, kalkulator prisma segi lima beraturan ini bisa jadi solusi praktisnya! Artikel ini akan membahas perancangan kalkulator tersebut secara konseptual, mulai dari algoritma hingga implementasi antarmuka.

Kita akan membahas langkah-langkah pembuatan kalkulator ini, dari perencanaan algoritma hingga pertimbangan desain antarmuka pengguna. Prosesnya mungkin terlihat rumit, tapi dengan pendekatan yang sistematis, kita bisa membuatnya lebih mudah dipahami.

Algoritma Perhitungan Luas Permukaan

Algoritma ini menghitung luas permukaan prisma segi lima beraturan dengan menjumlahkan luas alas dan luas sisi tegak. Rumus luas segi lima beraturan akan menjadi bagian penting dari perhitungan ini.

Berikut pseudocode untuk menghitung luas permukaan:

• Input: panjang sisi alas (s), tinggi prisma (h)
• Hitung luas alas (luas_alas) menggunakan rumus: luas_alas = (5/4) * s² * cot(π/5)
• Hitung keliling alas (keliling_alas): keliling_alas = 5 * s
• Hitung luas sisi tegak (luas_sisi_tegak): luas_sisi_tegak = keliling_alas * h
• Hitung luas permukaan total (luas_permukaan): luas_permukaan = 2 * luas_alas + luas_sisi_tegak
• Output: luas_permukaan

Algoritma Perhitungan Volume

Algoritma ini menghitung volume prisma segi lima beraturan dengan mengalikan luas alas dengan tinggi prisma. Perhitungan luas alas segi lima beraturan akan menjadi sub-algoritma yang terpisah.

Berikut pseudocode untuk menghitung volume:

• Input: panjang sisi alas (s), tinggi prisma (h)
• Panggil sub-algoritma perhitungan luas alas segi lima beraturan dengan input s, menghasilkan luas_alas
• Hitung volume (volume): volume = luas_alas * h
• Output: volume

Sub-algoritma perhitungan luas alas:

• Input: panjang sisi alas (s)
• Hitung luas alas (luas_alas): luas_alas = (5/4) * s² * cot(π/5)
• Output: luas_alas

Definisi Variabel

Tabel berikut menjelaskan variabel yang dibutuhkan dalam kalkulator:

Nama Variabel	Tipe Data	Deskripsi
s	double	Panjang sisi alas segi lima beraturan
h	double	Tinggi prisma
luas_alas	double	Luas alas segi lima beraturan
luas_permukaan	double	Luas permukaan total prisma
volume	double	Volume prisma

Flowchart Luas Permukaan

Flowchart ini akan menggambarkan alur perhitungan luas permukaan, dimulai dari input panjang sisi alas dan tinggi prisma, hingga menghasilkan output luas permukaan total. Secara visual, flowchart akan menunjukkan urutan langkah-langkah perhitungan, menggunakan simbol-simbol standar flowchart seperti bentuk persegi panjang untuk proses, bentuk jajaran genjang untuk input/output, dan bentuk belah ketupat untuk keputusan (jika ada).

Flowchart Volume

Mirip dengan flowchart luas permukaan, flowchart ini akan menggambarkan alur perhitungan volume, menunjukkan bagaimana luas alas dihitung terlebih dahulu sebelum dikalikan dengan tinggi prisma untuk mendapatkan volume. Flowchart akan menggambarkan dengan jelas alur perhitungan, termasuk pemanggilan sub-algoritma perhitungan luas alas.

Perhitungan Sudut

Kalkulator dapat dikembangkan untuk menghitung sudut-sudut dalam prisma segi lima beraturan. Sudut alas dapat dihitung dengan rumus sudut dalam segi lima beraturan (180*(5-2)/5 = 108 derajat). Sudut antara sisi tegak dan alas akan selalu 90 derajat karena sifat prisma tegak.

Perhitungan Diagonal

Menghitung diagonal sisi dan diagonal ruang membutuhkan rumus trigonometri. Diagonal sisi dapat dihitung menggunakan rumus s * (1 + √5)/2, sedangkan diagonal ruang memerlukan perhitungan yang lebih kompleks yang melibatkan teorema Pythagoras dalam tiga dimensi.

Implementasi Antarmuka

Antarmuka pengguna (GUI) yang sederhana dapat diimplementasikan menggunakan library Python seperti Tkinter atau PyQt. GUI akan mencakup field input untuk panjang sisi alas dan tinggi prisma, tombol “Hitung”, dan area display untuk menampilkan hasil perhitungan luas permukaan dan volume.

Penanganan Kesalahan

Kalkulator perlu menangani input yang salah, seperti nilai negatif untuk panjang sisi atau tinggi. Pesan kesalahan yang informatif, misalnya “Panjang sisi dan tinggi harus bernilai positif”, akan ditampilkan jika input tidak valid.

Rumus yang Digunakan

Berikut rumus-rumus matematika yang digunakan:

Rumus Luas Segi Lima Beraturan: Luas = (5/4) * s² * cot(π/5)
Rumus Volume Prisma: Volume = Luas Alas * Tinggi

Sejarah dan Perkembangan Konsep Prisma Segi Lima Beraturan

Prisma segi lima beraturan, dengan bentuknya yang unik dan simetris, menyimpan sejarah panjang dalam perkembangan geometri. Dari peradaban kuno hingga aplikasi modern di berbagai bidang sains dan teknologi, bentuk geometris ini telah memainkan peran penting dalam pemahaman kita tentang ruang dan bentuk. Mari kita telusuri perjalanan menarik konsep prisma segi lima beraturan ini.

Sejarah Penemuan dan Perkembangan Konsep

Meskipun sulit untuk menentukan secara pasti kapan tepatnya konsep prisma segi lima beraturan pertama kali ditemukan, jejaknya dapat ditelusuri hingga peradaban Yunani Kuno. Bangsa Yunani, dengan kecintaan mereka pada geometri dan keindahan proporsi, kemungkinan besar telah memahami dan menggunakan konsep ini dalam arsitektur dan seni mereka. Bukti arkeologis, meskipun tidak secara langsung menunjukkan prisma segi lima beraturan, menunjukkan pemahaman mereka akan bentuk-bentuk geometris yang kompleks. Perkembangan pemahaman tentang sifat-sifat geometrisnya, seperti rumus volume dan luas permukaan, berkembang secara bertahap. Definisi dasar muncul terlebih dahulu, diikuti oleh pengembangan rumus-rumus yang lebih kompleks seiring kemajuan matematika, terutama selama periode Renaisans dan era modern dengan munculnya kalkulus dan geometri analitik.

Tokoh-Tokoh Penting

Beberapa tokoh penting telah berkontribusi pada pemahaman kita tentang prisma segi lima beraturan. Kontribusi mereka tidak hanya sebatas definisi, tetapi juga mencakup aplikasi praktis dan pengembangan metode perhitungan yang lebih efisien.

Nama Tokoh	Periode Aktif	Kontribusi	Referensi Sumber
Euclid	~300 SM	Merupakan tokoh kunci dalam geometri klasik Yunani, karyanya “Elements” memberikan dasar pemahaman tentang bentuk-bentuk geometris, termasuk prisma. Meskipun tidak secara spesifik membahas prisma segi lima beraturan, prinsip-prinsip geometris yang ia kembangkan menjadi fondasi bagi pemahaman bentuk-bentuk tiga dimensi yang lebih kompleks.	Euclid. Elements.
Leonardo da Vinci	1452-1519	Sebagai seniman dan ilmuwan Renaisans, Da Vinci memiliki pemahaman yang mendalam tentang geometri dan proporsi. Karyanya menunjukkan penggunaan bentuk-bentuk geometris yang kompleks, dan pemahamannya tentang geometri ruang sangat mungkin mencakup prisma segi lima beraturan dalam konteks desain arsitektur atau karya seninya.	Various biographies and analyses of da Vinci’s works.
Isaac Newton	1643-1727	Kontribusi Newton dalam pengembangan kalkulus memberikan alat-alat matematika yang kuat untuk menghitung volume dan luas permukaan prisma segi lima beraturan dengan presisi tinggi. Pengembangan kalkulus integral memungkinkan perhitungan volume bangun ruang yang lebih kompleks.	Newton, I. (1687). Philosophiæ Naturalis Principia Mathematica.

Garis Waktu Perkembangan Pemahaman

Berikut adalah garis waktu singkat perkembangan pemahaman tentang prisma segi lima beraturan:

1. Zaman Yunani Kuno (~300 SM): Pemahaman dasar tentang bentuk-bentuk geometris, termasuk prisma, mulai berkembang. Prinsip-prinsip geometri Euclid memberikan landasan untuk memahami bentuk-bentuk tiga dimensi.
2. Renaisans (abad ke-15-16): Minat yang meningkat terhadap geometri dan seni memicu eksplorasi lebih lanjut tentang bentuk-bentuk geometris yang kompleks, termasuk prisma segi lima beraturan. Seniman dan arsitek menggunakannya dalam desain.
3. Era Pencerahan (abad ke-17-18): Pengembangan kalkulus oleh Newton dan Leibniz memberikan alat-alat matematika yang lebih canggih untuk menghitung volume dan luas permukaan prisma segi lima beraturan.
4. Abad ke-19 dan ke-20: Geometri analitik dan aljabar linear memberikan metode-metode baru untuk menganalisis prisma segi lima beraturan dan bentuk-bentuk geometris lainnya.
5. Era Modern: Aplikasi prisma segi lima beraturan meluas ke berbagai bidang, termasuk teknik sipil, arsitektur, dan desain industri.

Perkembangan Seiring Perkembangan Matematika

Perkembangan konsep prisma segi lima beraturan erat kaitannya dengan perkembangan geometri analitik dan kalkulus. Geometri analitik memungkinkan representasi prisma segi lima beraturan dalam sistem koordinat, memfasilitasi analisis yang lebih presisi. Kalkulus, khususnya kalkulus integral, memberikan metode untuk menghitung volume dan luas permukaan dengan akurasi tinggi. Metode perhitungan telah berevolusi dari pendekatan geometri klasik yang lebih intuitif menuju metode analitik yang lebih formal dan presisi.

Aplikasi dalam Ilmu Pengetahuan dan Teknologi

Prisma segi lima beraturan, meskipun mungkin tampak sederhana, memiliki berbagai aplikasi dalam ilmu pengetahuan dan teknologi.

• Arsitektur: Bentuk prisma segi lima beraturan dapat ditemukan dalam desain bangunan modern, baik untuk alasan estetika maupun struktural. Kubah-kubah dengan dasar segi lima, misalnya, dapat memanfaatkan sifat-sifat geometri prisma segi lima untuk distribusi beban yang optimal.
• Teknik Sipil: Dalam perencanaan infrastruktur, pemahaman tentang geometri prisma segi lima beraturan penting dalam perhitungan volume material yang dibutuhkan untuk proyek konstruksi seperti pembuatan bendungan atau konstruksi terowongan.
• Desain Industri: Bentuk prisma segi lima beraturan dapat digunakan dalam desain produk, misalnya pada kemasan atau komponen mesin, untuk menciptakan estetika yang unik dan efisiensi penggunaan material.

Kesalahan Umum dalam Memahami Prisma Segi Lima Beraturan

Prisma segi lima beraturan, dengan bentuknya yang unik dan rumit, seringkali menjadi momok bagi siswa dalam mempelajari geometri. Banyak konsep yang perlu dipahami, mulai dari menghitung luas permukaan hingga volume, dan kesalahan-kesalahan kecil bisa berakibat fatal pada hasil perhitungan. Artikel ini akan mengupas beberapa kesalahan umum yang sering terjadi dan memberikan tips jitu agar kamu nggak lagi galau menghadapi prisma segi lima beraturan!

Identifikasi Kesalahan Umum

Kesalahan dalam memahami prisma segi lima beraturan seringkali berakar pada pemahaman yang kurang tepat tentang sifat-sifat bangun ruang ini. Mulai dari keliru dalam mengidentifikasi jumlah sisi, rusuk, dan titik sudut, hingga salah dalam menghitung luas alas dan tinggi, semua bisa berujung pada hasil yang salah. Selain itu, kurangnya visualisasi bentuk tiga dimensi juga menjadi kendala utama. Bayangkan kamu mencoba menghitung volume tanpa bisa membayangkan bentuk prisma segi lima beraturan itu sendiri—sulit, bukan?

Cara Mengatasi Kesalahan Umum

Kuncinya adalah latihan dan pemahaman konsep yang kuat. Jangan hanya menghafal rumus, tapi pahami dari mana rumus tersebut berasal. Cobalah untuk membuat model prisma segi lima beraturan sendiri menggunakan kardus atau bahan lainnya. Visualisasi tiga dimensi akan sangat membantu dalam memahami konsep luas permukaan dan volume. Latihan soal secara rutin juga penting, mulai dari soal yang mudah hingga yang lebih kompleks. Jangan takut untuk salah, karena dari kesalahan itulah kita belajar!

Tabel Kesalahan Umum dan Cara Mengatasinya

Kesalahan Umum	Cara Mengatasi
Salah menghitung jumlah sisi, rusuk, dan titik sudut.	Ulangi definisi prisma segi lima beraturan dan hitung secara sistematis. Gunakan model fisik untuk membantu visualisasi.
Salah dalam menghitung luas alas.	Pecah alas menjadi beberapa segitiga dan hitung luas masing-masing segitiga, lalu jumlahkan. Pastikan memahami rumus luas segitiga dan penerapannya.
Menggunakan rumus yang salah untuk menghitung volume.	Pahami konsep volume sebagai luas alas dikalikan tinggi. Pastikan menggunakan rumus luas alas yang tepat untuk prisma segi lima beraturan.
Kesulitan memvisualisasikan bentuk tiga dimensi.	Gunakan model fisik, gambar, atau software geometri 3D untuk membantu visualisasi.
Tidak memahami hubungan antara elemen-elemen prisma segi lima beraturan.	Buat diagram dan label setiap elemen (sisi, rusuk, tinggi, alas) untuk memperjelas hubungan antar elemen.

Contoh Soal yang Sering Menimbulkan Kesalahan Pemahaman

Misalnya, soal yang meminta untuk menghitung volume prisma segi lima beraturan dengan panjang sisi alas 5 cm dan tinggi 10 cm. Kesalahan umum yang sering terjadi adalah salah menghitung luas alas. Banyak siswa yang keliru dalam menghitung luas segitiga penyusun alas, sehingga hasil akhirnya menjadi tidak akurat. Soal lain yang sering menimbulkan masalah adalah soal yang melibatkan perhitungan luas permukaan, dimana siswa seringkali lupa menghitung luas sisi tegak.

Strategi Pembelajaran yang Efektif

Untuk menghindari kesalahan-kesalahan tersebut, fokuslah pada pemahaman konsep dasar, bukan sekadar menghafal rumus. Gunakan berbagai metode pembelajaran, seperti visualisasi, manipulasi model fisik, dan diskusi kelompok. Jangan ragu untuk bertanya kepada guru atau teman jika mengalami kesulitan. Latihan soal secara konsisten dan analisis kesalahan yang telah dibuat juga sangat penting untuk meningkatkan pemahaman dan kemampuan menyelesaikan soal-soal prisma segi lima beraturan.

Perbandingan Prisma Segi Lima Beraturan dengan Bangun Ruang Sejenis Lainnya

Prisma segi lima beraturan, dengan bentuknya yang unik dan simetris, seringkali menarik perhatian dalam dunia geometri. Namun, bagaimana perbandingannya dengan bangun ruang sejenis lainnya? Artikel ini akan mengupas tuntas perbandingan prisma segi lima beraturan dengan prisma segi enam beraturan dan balok (prisma segi empat beraturan), meliputi luas permukaan, volume, jumlah sisi, dan simetri. Kita juga akan menganalisis pola yang muncul dari perbandingan ini dan melihat implikasinya dalam efisiensi penggunaan material.

Perbandingan Prisma Segi Lima Beraturan dengan Prisma Segi Enam Beraturan

Mari kita bandingkan prisma segi lima beraturan dengan prisma segi enam beraturan, keduanya dengan panjang rusuk alas 5 cm dan tinggi 10 cm. Perbedaan jumlah sisi akan berdampak pada luas permukaan dan volume.

Perhitungan Luas Permukaan dan Volume:

Prisma Segi Lima Beraturan:

Luas permukaan prisma segi lima = Luas alas + Luas sisi tegak = 5 x (1/2 x 5 x 5 x sin 72°) + 5 x 5 x 10 = 43,09 cm² + 250 cm² = 293,09 cm²

Volume prisma segi lima = Luas alas x tinggi = (1/2 x 5 x 5 x sin 72°) x 10 = 119,1 cm³

Prisma Segi Enam Beraturan:

Luas permukaan prisma segi enam = Luas alas + Luas sisi tegak = 6 x (1/2 x 5 x 5 x sin 60°) + 6 x 5 x 10 = 64,95 cm² + 300 cm² = 364,95 cm²

Volume prisma segi enam = Luas alas x tinggi = (6 x (1/2 x 5 x 5 x sin 60°)) x 10 = 108,25 cm³

Perbandingan Bentuk dan Simetri:

Prisma segi lima memiliki alas berbentuk segi lima beraturan, sementara prisma segi enam memiliki alas berbentuk segi enam beraturan. Keduanya memiliki sisi tegak berbentuk persegi panjang. Prisma segi lima memiliki 5 sumbu simetri, sedangkan prisma segi enam memiliki 6 sumbu simetri. Keduanya memiliki simetri putar.

Ilustrasi:

Bayangkan sebuah prisma segi lima seperti atap rumah yang memiliki 5 sisi miring, sedangkan prisma segi enam lebih mirip dengan sarang lebah yang memiliki 6 sisi.

Fitur	Prisma Segi Lima Beraturan (rusuk alas 5cm, tinggi 10cm)	Prisma Segi Enam Beraturan (rusuk alas 5cm, tinggi 10cm)
Jumlah Sisi Alas	5	6
Jumlah Sisi Tegak	5	6
Jumlah Titik Sudut	10	12
Luas Permukaan	293,09 cm²	364,95 cm²
Volume	119,1 cm³	108,25 cm³
Jenis Simetri	5 sumbu simetri, simetri putar	6 sumbu simetri, simetri putar

Perbandingan Prisma Segi Lima Beraturan dengan Balok

Selanjutnya, mari kita bandingkan prisma segi lima beraturan dengan balok (prisma segi empat beraturan) dengan panjang 5 cm, lebar 5 cm, dan tinggi 10 cm.

Perhitungan Luas Permukaan dan Volume Balok:

Luas permukaan balok = 2(panjang x lebar + panjang x tinggi + lebar x tinggi) = 2(5 x 5 + 5 x 10 + 5 x 10) = 2(25 + 50 + 50) = 250 cm²

Volume balok = panjang x lebar x tinggi = 5 x 5 x 10 = 250 cm³

Perbandingan Bentuk dan Simetri:

Balok memiliki alas berbentuk persegi, sementara prisma segi lima memiliki alas berbentuk segi lima beraturan. Balok memiliki 3 pasang sisi yang sama dan sejajar, sedangkan prisma segi lima memiliki 5 sisi tegak yang sama dan sejajar. Balok memiliki lebih banyak bidang simetri dibandingkan prisma segi lima.

Contoh Penerapan:

Balok sering kita jumpai dalam bentuk kotak kemasan, buku, atau ruangan. Prisma segi lima bisa dijumpai pada desain atap rumah tertentu atau struktur bangunan yang unik.

Fitur	Prisma Segi Lima Beraturan (rusuk alas 5cm, tinggi 10cm)	Balok (p=5cm, l=5cm, t=10cm)
Jumlah Sisi Alas	5	4
Jumlah Sisi Tegak	5	4
Jumlah Titik Sudut	10	8
Luas Permukaan	293,09 cm²	250 cm²
Volume	119,1 cm³	250 cm³
Jenis Simetri	5 sumbu simetri, simetri putar	3 bidang simetri, simetri putar
Contoh Penerapan	Atap rumah, struktur bangunan	Kotak kemasan, buku, ruangan

Analisis Pola Perbandingan Luas Permukaan dan Volume

Dari perbandingan di atas, terlihat bahwa seiring bertambahnya jumlah sisi alas, luas permukaan cenderung meningkat. Namun, hubungan antara jumlah sisi alas dan efisiensi penggunaan material untuk volume yang sama tidak selalu linier. Meskipun prisma segi enam memiliki volume yang lebih kecil daripada balok dengan ukuran yang sama, luas permukaannya lebih besar. Ini menunjukkan bahwa bentuk yang lebih kompleks (dengan lebih banyak sisi) tidak selalu lebih efisien dalam penggunaan material untuk mencapai volume tertentu.

Penerapan Geometri Analitik pada Prisma Segi Lima Beraturan

Prisma segi lima beraturan, dengan bentuknya yang unik dan simetris, bisa didekati dengan lebih mudah dan akurat menggunakan geometri analitik. Bayangkan saja, bentuk tiga dimensi yang rumit ini bisa direpresentasikan dengan angka-angka sederhana dalam sistem koordinat kartesian! Geometri analitik membuka jalan untuk perhitungan yang presisi, dari menghitung jarak antar titik hingga menganalisis volume dan luas permukaan. Yuk, kita kupas tuntas bagaimana geometri analitik membantu kita memahami prisma segi lima beraturan lebih dalam!

Representasi Prisma Segi Lima Beraturan dalam Koordinat Kartesian

Untuk merepresentasikan prisma segi lima beraturan dalam sistem koordinat kartesian, kita bisa memulai dengan menentukan titik-titik sudut alasnya. Misalnya, kita bisa menempatkan salah satu titik sudut di titik asal (0, 0, 0). Kemudian, dengan menggunakan panjang sisi alas dan tinggi prisma, kita bisa menghitung koordinat kartesian dari semua titik sudut lainnya. Perlu diingat bahwa kunci utama di sini adalah kesimetrisan prisma segi lima beraturan yang membantu menyederhanakan proses penentuan koordinat.

Contoh Perhitungan Jarak Antar Titik

Misalkan kita punya prisma segi lima beraturan dengan panjang sisi alas 5 cm dan tinggi 10 cm. Jika titik A berada di (0, 0, 0) dan titik B berada di puncak prisma tepat di atas titik A, maka koordinat B adalah (0, 0, 10). Jarak antara A dan B? Gampang! Dengan rumus jarak antara dua titik dalam ruang tiga dimensi, √((x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²) , kita dapatkan jaraknya adalah 10 cm. Perhitungan jarak antar titik lainnya bisa dilakukan dengan cara yang serupa, dengan terlebih dahulu menentukan koordinat masing-masing titik.

Penerapan Vektor dalam Analisis Prisma Segi Lima Beraturan

Vektor memberikan cara yang elegan untuk menganalisis prisma segi lima beraturan. Kita bisa merepresentasikan sisi-sisi prisma sebagai vektor, dan menggunakan operasi vektor seperti penjumlahan, pengurangan, dan perkalian skalar untuk menghitung berbagai besaran geometri, seperti luas permukaan dan volume. Misalnya, perkalian silang antara dua vektor yang merepresentasikan sisi alas dapat digunakan untuk menghitung luas alas prisma.

Rumus Geometri Analitik yang Relevan

• Rumus jarak antara dua titik dalam ruang tiga dimensi:
  

  √((x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²)

• Rumus perkalian skalar dua vektor:
  

  a . b = |a||b|cosθ

• Rumus perkalian silang dua vektor:
  

  a x b = |a||b|sinθn

• Rumus volume prisma:
  

  Volume = Luas Alas x Tinggi

Kelebihan dan Kekurangan Penggunaan Geometri Analitik

Geometri analitik menawarkan presisi dan ketelitian tinggi dalam menganalisis prisma segi lima beraturan. Kita bisa melakukan perhitungan yang kompleks dengan mudah dan mendapatkan hasil yang akurat. Namun, penerapannya bisa menjadi rumit jika prisma tersebut memiliki ukuran yang sangat besar atau bentuk yang tidak beraturan. Selain itu, dibutuhkan pemahaman yang kuat tentang aljabar dan trigonometri untuk dapat menerapkan geometri analitik secara efektif.

Penggunaan Software untuk Memvisualisasikan Prisma Segi Lima Beraturan

Visualisasi geometri tiga dimensi, khususnya bangun ruang seperti prisma segi lima beraturan, seringkali terasa rumit hanya dengan mengandalkan imajinasi. Untungnya, di era digital ini kita punya senjata ampuh: software geometri 3D! Software ini tak hanya memudahkan visualisasi, tapi juga membantu kita menganalisis berbagai aspek prisma segi lima beraturan dengan lebih akurat dan efisien. Bayangkan bisa memutar, memperbesar, bahkan mengukur setiap sisi dan sudutnya secara virtual—keren, kan?

Software untuk Memvisualisasikan Prisma Segi Lima Beraturan

Ada beberapa software yang bisa kamu gunakan untuk memvisualisasikan prisma segi lima beraturan, mulai dari yang berbayar hingga yang gratis dan open source. Masing-masing memiliki kelebihan dan kekurangannya tersendiri, tergantung kebutuhan dan tingkat keahlianmu.

• GeoGebra: Software ini terkenal ramah pengguna dan gratis, cocok untuk pemula. GeoGebra memungkinkan pembuatan model 3D yang interaktif dan mudah dimodifikasi.
• Autodesk Fusion 360: Software yang lebih powerful dan berbayar ini menawarkan fitur yang lebih lengkap, termasuk kemampuan untuk melakukan simulasi dan analisis desain. Cocok untuk yang butuh visualisasi yang lebih detail dan presisi.
• Blender: Software open source yang sangat populer di kalangan animator dan desainer 3D. Meskipun memiliki kurva pembelajaran yang lebih curam, Blender menawarkan fleksibilitas dan kemampuan yang luar biasa untuk menciptakan model 3D yang sangat realistis.
• SketchUp: Software yang relatif mudah digunakan dan populer di kalangan arsitek dan desainer. Memungkinkan pembuatan model 3D yang akurat dan detail.

Langkah-Langkah Membuat Model Prisma Segi Lima Beraturan

Secara umum, langkah-langkah membuat model prisma segi lima beraturan di software geometri 3D cukup mirip. Perbedaannya terletak pada antarmuka dan fitur spesifik masing-masing software. Berikut gambaran umum langkah-langkahnya:

1. Buat alas segi lima beraturan: Gunakan tool yang tersedia di software untuk membuat poligon beraturan dengan lima sisi yang sama panjang.
2. Buat sisi tegak: Buat garis tegak lurus dari setiap titik sudut alas segi lima ke atas dengan tinggi yang sama.
3. Hubungkan titik-titik: Hubungkan titik-titik ujung garis tegak lurus tersebut untuk membentuk sisi tegak prisma.
4. Tambahkan detail (opsional): Berikan tekstur, warna, atau detail lain untuk membuat model prisma lebih menarik dan informatif.

Kelebihan dan Kekurangan Penggunaan Software

Penggunaan software geometri 3D untuk memvisualisasikan prisma segi lima beraturan memiliki kelebihan dan kekurangan.

Kelebihan	Kekurangan
Visualisasi yang lebih akurat dan detail	Membutuhkan keterampilan dan waktu untuk mempelajari software
Kemudahan dalam melakukan manipulasi dan analisis	Software berbayar bisa mahal
Memungkinkan pembuatan model yang interaktif	Ketergantungan pada perangkat keras dan software

Contoh Skenario Penggunaan Software

Bayangkan seorang guru matematika menggunakan GeoGebra untuk menunjukkan kepada siswanya bagaimana menghitung volume prisma segi lima beraturan. Dengan memutar dan memperbesar model 3D, siswa dapat lebih mudah memahami konsep dan rumus yang diajarkan. Software ini juga bisa digunakan untuk menganalisis pengaruh perubahan tinggi atau panjang sisi alas terhadap volume prisma, atau untuk membandingkan volume prisma segi lima beraturan dengan bangun ruang lainnya.

Variasi Prisma Segi Lima (tidak beraturan)

Setelah membahas prisma segi lima beraturan yang rapi dan simetris, saatnya kita menyelami dunia prisma segi lima yang lebih… liar! Yap, kita akan ngobrolin prisma segi lima tak beraturan. Bentuknya nggak se-perfect prisma beraturan, tapi justru di situ serunya. Perbedaannya? Bagaimana cara menghitungnya? Simak penjelasannya di bawah ini!

Perbedaan Prisma Segi Lima Beraturan dan Tidak Beraturan

Perbedaan utama terletak pada bentuk alasnya. Prisma segi lima beraturan memiliki alas berupa segi lima beraturan, di mana semua sisi dan sudutnya sama panjang dan besar. Bayangkan bintang laut yang sempurna! Sementara itu, prisma segi lima tidak beraturan memiliki alas berupa segi lima tidak beraturan – sisi dan sudutnya memiliki panjang dan besar yang berbeda-beda. Coba bayangkan bintang laut yang… agak lecet.

Contoh Prisma Segi Lima Tidak Beraturan

Contohnya banyak banget di sekitar kita, lho! Bayangkan sebuah rumah yang atapnya berbentuk prisma segi lima tidak beraturan. Atau mungkin potongan batu yang secara alami membentuk prisma segi lima tidak beraturan. Bahkan, beberapa desain furnitur modern juga terinspirasi dari bentuk geometri ini, menciptakan tampilan yang unik dan menarik.

Perbandingan Rumus Perhitungan Luas Permukaan dan Volume

Nah, ini dia bagian yang sedikit lebih menantang. Untuk prisma segi lima beraturan, perhitungan luas permukaan dan volume relatif mudah karena bentuknya yang teratur. Kita bisa menggunakan rumus-rumus standar. Tapi untuk prisma segi lima tidak beraturan? Kita perlu sedikit lebih kreatif.

Untuk menghitung luas permukaan, kita perlu menghitung luas masing-masing sisi (termasuk alas dan atap) secara terpisah, lalu menjumlahkannya. Untuk volume, kita bisa membagi prisma menjadi beberapa bagian yang lebih sederhana, menghitung volume masing-masing bagian, lalu menjumlahkannya. Atau, kita bisa menggunakan kalkulus integral untuk pendekatan yang lebih akurat.

Luas Permukaan Prisma (umum): Jumlah luas semua sisi.
Volume Prisma (umum): Luas alas x tinggi.

Rumus-rumus di atas berlaku secara umum, tetapi untuk prisma segi lima tidak beraturan, kita perlu menentukan luas alas dan tinggi dengan cara yang lebih kompleks, mungkin dengan memecah bentuk alas menjadi segitiga-segitiga.

Ilustrasi Prisma Segi Lima Tidak Beraturan

Bayangkan sebuah prisma dengan alas berbentuk segi lima yang agak “menyimpang”. Salah satu sisinya lebih panjang, sudut-sudutnya tidak sama besar, dan secara keseluruhan bentuknya tidak simetris. Tinggi prisma tetap tegak lurus terhadap alasnya. Bentuk ini jauh lebih kompleks dibandingkan dengan prisma segi lima beraturan yang sempurna.

Kesulitan Menghitung Luas Permukaan dan Volume Prisma Segi Lima Tidak Beraturan

Tantangan utama terletak pada ketidakberaturan bentuk alasnya. Tidak ada rumus sederhana yang bisa langsung diaplikasikan. Kita perlu melakukan pendekatan yang lebih rumit, seperti membagi alas menjadi beberapa segitiga atau menggunakan trigonometri untuk menghitung panjang dan sudut yang diperlukan. Akurasi hasil perhitungan juga sangat bergantung pada ketelitian pengukuran dan metode perhitungan yang digunakan. Prosesnya lebih kompleks dan membutuhkan pemahaman yang lebih mendalam tentang geometri dan trigonometri.

Terakhir

Perjalanan kita menjelajahi dunia prisma segi lima beraturan telah sampai di penghujung. Dari definisi hingga aplikasi di dunia nyata, kita telah menyaksikan keindahan dan kompleksitas bentuk geometri ini. Lebih dari sekadar bangun ruang, prisma segi lima beraturan merupakan bukti nyata bagaimana matematika mampu menciptakan bentuk-bentuk yang menakjubkan dan bermanfaat. Semoga pemahaman kita tentang prisma segi lima beraturan semakin dalam dan menginspirasi kita untuk terus mengeksplorasi keajaiban matematika!