Menjelajah Perkalian yang Hasilnya 81

Perkalian yang hasilnya 81? Bukan cuma soal hitung-hitungan biasa, lho! Angka 81 menyimpan banyak misteri matematika yang menarik untuk diungkap. Dari faktorisasi prima hingga kombinasi perkalian yang unik, angka ini punya segudang kejutan yang siap mengasah otak kita. Siap-siap tercengang dengan berbagai cara untuk mendapatkan hasil perkalian 81!

Kita akan menjelajahi berbagai metode untuk mencapai angka 81 melalui perkalian, mulai dari perkalian sederhana hingga penggunaan bilangan pecahan dan negatif. Simak juga bagaimana angka 81 berinteraksi dengan sistem bilangan biner dan heksadesimal, serta eksplorasi pola-pola bilangan yang mengarah pada hasil perkalian 81. Petualangan matematika kita akan membuka wawasan baru tentang angka yang tampak sederhana ini.

Faktor Perkalian 81

Angka 81, kelihatannya sederhana, ya? Tapi di balik kesederhanaannya, tersimpan misteri perkalian yang menarik untuk diungkap. Kita akan menyelami dunia faktor-faktor 81, mengungkap pasangan-pasangannya, dan mengklasifikasikannya. Siap-siap me-refresh pengetahuan matematika kamu!

Daftar Faktor Bilangan 81

Faktor dari 81 adalah bilangan bulat yang dapat membagi 81 tanpa sisa. Berikut daftar lengkapnya, disusun secara menaik:

1. 1
2. 3
3. 9
4. 27
5. 81

Pasangan Faktor dan Hubungannya dengan 81

Setiap faktor dalam daftar di atas memiliki pasangan yang jika dikalikan akan menghasilkan 81. Berikut tabel yang menunjukkan pasangan-pasangan tersebut beserta penjelasannya:

Faktor	Pasangan Faktor	Jenis Faktor	Contoh Perkalian
1	81	1: Prima, 81: Komposit	1 * 81 = 81
3	27	Keduanya: Prima	3 * 27 = 81
9	9	Komposit	9 * 9 = 81

Klasifikasi Bilangan 81

Berdasarkan faktor-faktornya, 81 diklasifikasikan sebagai bilangan komposit karena memiliki lebih dari dua faktor. Ia bukan bilangan prima (hanya memiliki dua faktor, 1 dan dirinya sendiri) dan juga bukan bilangan sempurna (jumlah faktornya selain dirinya sendiri tidak sama dengan dirinya sendiri).

Faktorisasi Prima 81

Faktorisasi prima dari 81 adalah 3 x 3 x 3 x 3 atau 3⁴. Bayangkan sebuah diagram pohon faktorisasi: di puncaknya angka 81, kemudian bercabang menjadi 9 x 9, lalu masing-masing 9 bercabang lagi menjadi 3 x 3. Semua cabang akhirnya berakhir pada angka prima 3.

Faktor Kuadrat Sempurna dan Faktor Ganjil/Genap

Faktor 9 dari 81 merupakan bilangan kuadrat sempurna (9 = 3²). Semua faktor 81 (1, 3, 9, 27, 81) adalah bilangan ganjil, sehingga tidak ada faktor genap.

Kombinasi Perkalian Menuju 81

Angka 81, kelihatannya sederhana, ya? Tapi coba deh kita ulik lebih dalam. Ternyata, ada banyak banget kombinasi perkalian yang menghasilkan angka ajaib ini. Dari perkalian sederhana sampai yang sedikit lebih rumit, semuanya menuju satu tujuan: angka 81! Siap-siap otakmu diuji dengan beberapa kombinasi perkalian yang mungkin belum pernah kamu pikirkan sebelumnya.

Berikut ini beberapa contoh kombinasi perkalian yang menghasilkan 81, menunjukkan fleksibilitas operasi perkalian dalam matematika. Kita akan menggunakan bilangan bulat positif untuk memudahkan pemahaman, tapi nanti kita juga akan mencoba dengan bilangan desimal.

Lima Kombinasi Perkalian Bilangan Bulat Positif yang Menghasilkan 81

• 9 x 9 = 81. Ini adalah kombinasi paling klasik dan mudah diingat. Perkalian dua angka yang sama menghasilkan 81. Simpel, kan?
• 27 x 3 = 81. Kombinasi ini menunjukkan perkalian dengan bilangan yang lebih besar dan lebih kecil, tetap menghasilkan angka yang sama.
• 81 x 1 = 81. Ini adalah kombinasi yang paling dasar, perkalian dengan angka satu selalu menghasilkan angka itu sendiri.
• 3 x 27 = 81. Sama seperti poin kedua, namun urutan perkaliannya dibalik. Menunjukkan sifat komutatif perkalian (a x b = b x a).
• (-9) x (-9) = 81. Meskipun kita fokus pada bilangan bulat positif, perlu diingat bahwa perkalian dua bilangan negatif juga menghasilkan bilangan positif. Ini adalah contoh menarik dari aturan perkalian bilangan negatif.

Contoh Kombinasi Perkalian dengan Bilangan Desimal

Tidak hanya bilangan bulat, perkalian dengan bilangan desimal pun bisa menghasilkan 81. Mari kita lihat contohnya:

• 27 x 3.0 = 81. Contoh ini menunjukkan bahwa mengalikan bilangan bulat dengan bilangan desimal (dengan angka di belakang koma nol) tetap menghasilkan hasil yang sama dengan perkalian bilangan bulat.
• 9.0 x 9.0 = 81. Sama seperti poin pertama, namun kedua bilangan merupakan bilangan desimal dengan angka di belakang koma nol.
• 10.125 x 8 = 81. Contoh ini menunjukkan kombinasi perkalian yang melibatkan bilangan desimal dengan lebih dari satu angka di belakang koma.

Pangkat dan Akar 81

Angka 81, sekilas terlihat biasa saja. Tapi, kalau kita ‘bongkar’ lebih dalam, angka ini menyimpan rahasia menarik terkait pangkat dan akar. Kita akan mengulik bagaimana angka 81 bisa dihasilkan dari operasi pangkat, dan bagaimana mencari akarnya. Siap-siap me-level up pemahaman matematika kamu!

Pangkat yang Menghasilkan 81

Nah, untuk mendapatkan 81, kita bisa menggunakan operasi pangkat. Pertanyaannya, pangkat berapakah yang menghasilkan 81? Jawabannya nggak cuma satu, lho! Kita bisa menggunakan pangkat dua (kuadrat) atau pangkat empat. 9 pangkat 2 (9²) sama dengan 81, dan 3 pangkat 4 (3⁴) juga sama dengan 81. Gimana, mulai seru kan?

Akar Kuadrat dari 81

Setelah kita tahu pangkatnya, sekarang saatnya kita cari akar kuadratnya. Akar kuadrat adalah kebalikan dari pangkat dua. Jadi, akar kuadrat dari 81 adalah angka yang jika dikuadratkan (dikalikan sendiri) hasilnya 81. Jawabannya adalah 9, karena 9 x 9 = 81.

Hubungan Pangkat dan Akar pada Bilangan 81

Ada hubungan yang erat antara pangkat dan akar. Bisa dibilang, mereka adalah dua sisi mata uang yang sama. Jika 9² = 81, maka √81 = 9. Operasi pangkat dan akar saling membalikkan. Ini berlaku untuk semua bilangan, bukan cuma 81.

Ilustrasi Hubungan 81, Akar Kuadrat, dan Pangkat

Bayangkan sebuah persegi dengan luas 81 satuan persegi. Panjang sisi persegi tersebut adalah akar kuadrat dari 81, yaitu 9 satuan. Jika kita memandang angka 9 sebagai alas dan 9 sebagai tinggi, maka luas persegi tersebut adalah 9 x 9 = 81. Jadi, 9 adalah akar kuadrat dari 81, dan 9² adalah pangkat dua yang menghasilkan 81. Kita juga bisa membayangkan kubus dengan volume 81 satuan kubik, akan tetapi ilustrasi persegi lebih mudah dipahami dalam konteks akar kuadrat.

Contoh Perhitungan Pangkat dan Akar Lain yang Menghasilkan 81

Selain 9² dan 3⁴, ada kemungkinan kombinasi lain, walau mungkin tidak se-straightforward. Misalnya, kita bisa menggunakan pecahan atau bilangan desimal. Namun, untuk contoh yang sederhana dan mudah dipahami, 9² dan 3⁴ adalah yang paling representatif. Mencari kombinasi lain bisa menjadi tantangan tersendiri, tapi intinya tetap sama: operasi pangkat dan akar saling berelasi untuk menghasilkan angka 81.

Perkalian Berurutan Menuju 81

Angka 81, kelihatannya sederhana, ya? Tapi coba deh kita ulik lebih dalam. Ternyata, angka ini menyimpan segudang kemungkinan kombinasi perkalian berurutan! Kita bisa mencapai 81 dengan berbagai langkah, menggunakan angka-angka yang berbeda. Perjalanan menuju 81 ini bak petualangan matematika yang seru dan penuh kejutan. Siap-siap tercengang dengan berbagai kemungkinan yang akan kita eksplor!

Rangkaian Perkalian Berurutan Menuju 81

Berikut ini tiga rangkaian perkalian berurutan yang menghasilkan 81, dengan jumlah langkah yang berbeda-beda. Kita akan melihat bagaimana setiap langkah saling berkaitan dan membentuk sebuah pola yang menarik. Siapkan kalkulatormu, atau mungkin cukup pakai jari aja, kalau kamu jago ngitung cepat!

Rangkaian Perkalian 3 Langkah

Langkah	Operasi	Hasil
1	3 x 3	9
2	9 x 3	27
3	27 x 3	81

Flowchart: Mulai -> 3 x 3 = 9 -> 9 x 3 = 27 -> 27 x 3 = 81 -> Selesai. Ilustrasi: Bayangkan tiga kotak kecil membentuk kotak lebih besar, lalu tiga kotak besar membentuk kotak yang lebih besar lagi, dan akhirnya tiga kotak besar itu membentuk kotak raksasa yang mewakili angka 81. Setiap kotak mewakili hasil perkalian di setiap langkah.

Rangkaian Perkalian 4 Langkah

Langkah	Operasi	Hasil
1	3 x 3	9
2	9 x 1	9
3	9 x 3	27
4	27 x 3	81

Flowchart: Mulai -> 3 x 3 = 9 -> 9 x 1 = 9 -> 9 x 3 = 27 -> 27 x 3 = 81 -> Selesai. Ilustrasi: Kita bisa membayangkan sebuah pohon yang bercabang. Batang pohon mewakili angka 3, cabang pertama mewakili perkalian 3×3, lalu cabang kedua mewakili perkalian 9×1, dan seterusnya hingga mencapai buah di ujung cabang terakhir yang bernilai 81.

Rangkaian Perkalian 5 Langkah

Langkah	Operasi	Hasil
1	1 x 9	9
2	9 x 1	9
3	9 x 3	27
4	27 x 1	27
5	27 x 3	81

Flowchart: Mulai -> 1 x 9 = 9 -> 9 x 1 = 9 -> 9 x 3 = 27 -> 27 x 1 = 27 -> 27 x 3 = 81 -> Selesai. Ilustrasi: Visualisasikan ini sebagai perjalanan kereta api. Setiap gerbong mewakili langkah perkalian, dan angka di setiap gerbong menunjukkan hasil perkalian. Perjalanan berakhir di stasiun 81.

Rangkaian Perkalian dengan Bilangan Desimal

Mencari kombinasi perkalian dengan bilangan desimal ternyata lebih menantang! Berikut contohnya:

1. 9 x 9 = 81
2. 4.5 x 18 = 81
3. 2.25 x 36 = 81

Strategi Menemukan Rangkaian Perkalian

Strategi yang efektif adalah dengan memulai dari faktor-faktor utama dari 81, yaitu 3 dan 9. Kemudian, kita bisa memanipulasi angka-angka tersebut dengan menambahkan perkalian dengan 1 untuk memperpanjang langkah perkalian, atau menggunakan perkalian dengan angka lain yang menghasilkan faktor dari 81. Metode ini efektif karena kita memulai dari dasar yang kuat dan membangun rangkaian perkalian secara sistematis.

Puisi Perkalian 81

Delapan puluh satu, angka yang elok,
Berbagai cara tuk diracik, terpatri kokoh.
Perkalian beruntun, langkah demi langkah,
Menghasilkan angka ajaib, terukir indah.

Keterbatasan Metode

Metode ini memiliki keterbatasan dalam hal jumlah langkah perkalian yang bisa digunakan. Semakin banyak langkah yang diinginkan, semakin kompleks pencarian kombinasinya. Penggunaan bilangan negatif juga akan memperluas kemungkinan kombinasi, tetapi akan membuat proses pencarian menjadi lebih rumit dan membutuhkan pertimbangan khusus terkait tanda positif dan negatif dalam perkalian.

Perkalian dengan Bilangan Pecahan yang Hasilnya 81

Siapa sangka, angka 81 yang terlihat sederhana bisa dihasilkan dari berbagai macam perkalian bilangan pecahan? Bayangkan saja, kombinasi pecahan biasa, pecahan campuran, bahkan perkalian dengan bilangan bulat bisa menghasilkan angka yang sama! Yuk, kita bongkar rahasia di balik perkalian-perkalian unik ini.

Perkalian bilangan pecahan memang terlihat rumit, tapi sebenarnya asyik banget kalau kita udah paham caranya. Kuncinya ada di penyederhanaan pecahan dan pemahaman tentang urutan operasi. Dengan sedikit trik dan latihan, kamu pasti bisa menguasainya!

Contoh Perkalian Bilangan Pecahan yang Hasilnya 81

Berikut ini tiga contoh soal perkalian bilangan pecahan yang menghasilkan 81, lengkap dengan langkah-langkah penyelesaiannya. Siap-siap tercengang dengan keunikannya!

Contoh Soal	Langkah Perhitungan	Hasil Akhir (dalam bentuk paling sederhana)
Contoh 1: Pecahan Campuran x Pecahan Biasa = 81	2 1/2 x 32 2/3 = (5/2) x (100/3) = 500/6 = 250/3 = 83 1/3 (Oops, sepertinya ada kesalahan di contoh ini. Mari kita coba contoh lain yang hasilnya benar-benar 81) Mari kita coba 27/1 x 3/1 = 81	81
Contoh 2: Pecahan Biasa x Bilangan Bulat = 81	(81/1) x 1 = 81	81
Contoh 3: Pecahan Campuran x Pecahan Campuran = 81	9 x 9 = 81 (Atau kita bisa menggunakan pecahan campuran lain, misalnya: 4 1/2 x 18 = (9/2) x 18 = 81)	81

Gimana? Lumayan menantang, kan? Tapi dengan memahami konsep dasar pecahan dan perkalian, semua soal ini bisa dipecahkan dengan mudah.

Contoh Tambahan Perkalian Bilangan Pecahan yang Hasilnya 81

Berikut dua contoh tambahan perkalian bilangan pecahan yang hasilnya 81, tanpa langkah perhitungan. Cobalah untuk menyelesaikannya sendiri sebagai latihan!

• Contoh Tambahan 1: (27/1) x 3 = 81
• Contoh Tambahan 2: (9/1) x (9/1) = 81

Penyederhanaan Pecahan dalam Perkalian Bilangan Pecahan

Penyederhanaan pecahan sangat penting dalam perkalian bilangan pecahan untuk mendapatkan hasil yang paling sederhana dan mudah dipahami. Salah satu metode yang efektif adalah dengan menggunakan pemfaktoran prima. Kita uraikan setiap bilangan menjadi faktor-faktor primanya, kemudian menyederhanakan pecahan dengan membagi pembilang dan penyebut dengan faktor-faktor prima yang sama.

Contoh: Sederhanakan pecahan 18/24. Faktor prima dari 18 adalah 2 x 3 x 3, dan faktor prima dari 24 adalah 2 x 2 x 2 x 3. Kita bisa menyederhanakan pecahan tersebut menjadi (2 x 3 x 3) / (2 x 2 x 2 x 3) = 3/4.

Perkalian dengan Bilangan Negatif yang menghasilkan 81

Siapa sangka, perkalian nggak cuma soal angka-angka positif yang manis? Dunia bilangan negatif juga punya pesonanya sendiri, lho! Kali ini, kita akan menjelajahi bagaimana perkalian bilangan negatif bisa menghasilkan angka 81. Siap-siap otakmu di-challenge!

Aturan Perkalian Bilangan Negatif

Sebelum kita terjun ke contoh-contohnya, mari kita ingat kembali aturan dasar perkalian bilangan negatif. Intinya gampang kok, cuma ada dua hal yang perlu kamu ingat: Perkalian dua bilangan negatif menghasilkan bilangan positif, sedangkan perkalian bilangan negatif dan positif menghasilkan bilangan negatif. Bayangkan seperti ini: min (-) kali min (-) sama dengan plus (+), sedangkan min (-) kali plus (+) sama dengan min (-). Gampang, kan?

Contoh Perkalian Bilangan Negatif yang Menghasilkan 81

Sekarang, saatnya kita lihat aksi nyata! Berikut beberapa contoh perkalian bilangan negatif yang hasilnya 81. Perhatikan baik-baik tanda positif dan negatifnya, ya!

Bilangan Pertama	Bilangan Kedua	Hasil	Penjelasan Tanda Hasil
-9	-9	81	Negatif kali negatif sama dengan positif.
-27	-3	81	Negatif kali negatif sama dengan positif.
-81	-1	81	Negatif kali negatif sama dengan positif.

Sebagai contoh tambahan, perkalian bilangan negatif dengan pecahan juga bisa menghasilkan 81. Misalnya, (-27/1) x (-3) = 81. Atau, (-9/1) x (-9) = 81.

Ringkasan Aturan Perkalian Bilangan Negatif:

• Negatif x Negatif = Positif
• Negatif x Positif = Negatif
• Positif x Negatif = Negatif

Soal Latihan

Yuk, kita uji pemahamanmu! Tentukan dua bilangan negatif yang jika dikalikan menghasilkan 81.

Jawaban: -9 dan -9

Soal Cerita

Suhu di puncak gunung pada siang hari adalah 0 derajat Celcius. Setiap jam, suhu turun 9 derajat Celcius. Berapa derajat Celcius suhu di puncak gunung setelah 9 jam?

Penyelesaian: Suhu turun 9 derajat Celcius selama 9 jam, sehingga penurunan suhu total adalah -9 x 9 = -81 derajat Celcius. Karena suhu awal 0 derajat Celcius, maka suhu setelah 9 jam adalah 0 + (-81) = -81 derajat Celcius. Namun, pertanyaan meminta berapa derajat Celcius suhu di puncak gunung setelah 9 jam, sehingga kita perlu mengabaikan tanda negatif. Jadi, suhu setelah 9 jam adalah 81 derajat Celcius di bawah 0.

Hubungan dengan Invers Perkalian

Perkalian bilangan negatif berhubungan erat dengan konsep invers perkalian. Invers perkalian dari suatu bilangan adalah bilangan yang jika dikalikan dengan bilangan tersebut menghasilkan 1. Misalnya, invers perkalian dari 9 adalah 1/9, karena 9 x (1/9) = 1. Begitu pula dengan bilangan negatif, invers perkalian dari -9 adalah -1/9, karena (-9) x (-1/9) = 1.

Contoh Perkalian Bilangan Negatif yang Menghasilkan -81

Sekarang, mari kita coba dengan hasil -81. Perhatikan bagaimana tanda negatif mempengaruhi hasil perkalian.

Bilangan Pertama	Bilangan Kedua	Hasil	Penjelasan Tanda Hasil
9	-9	-81	Positif kali negatif sama dengan negatif.
-9	9	-81	Negatif kali positif sama dengan negatif.
27	-3	-81	Positif kali negatif sama dengan negatif.

Penerapan Perkalian 81 dalam Masalah Konkret

Perkalian, khususnya perkalian dengan angka 81, bukan cuma soal angka-angka di buku teks. Di dunia nyata, perkalian ini sering muncul dalam berbagai situasi, dari menghitung jumlah barang hingga menyelesaikan masalah geometri. Yuk, kita lihat beberapa contoh penerapannya!

Contoh Soal Cerita Pertama dan Penyelesaiannya

Bayangkan kamu punya 9 kotak berisi permen. Setiap kotak berisi 9 permen. Berapa total jumlah permen yang kamu miliki?

Untuk menyelesaikannya, kita perlu melakukan perkalian: 9 kotak x 9 permen/kotak = 81 permen. Jadi, kamu memiliki total 81 permen. Perkalian 9 x 9 = 81 digunakan untuk menghitung total jumlah permen dari seluruh kotak.

Contoh Soal Cerita Kedua dan Penyelesaiannya

Sebuah toko buku sedang mengadakan promo buku komik. Terdapat 27 rak buku, dan setiap rak berisi 3 tumpuk komik. Setiap tumpuk berisi 3 komik. Berapa total komik yang ada di toko buku tersebut?

Langkah pertama, kita hitung jumlah komik per rak: 3 tumpuk x 3 komik/tumpuk = 9 komik/rak. Kemudian, kita kalikan dengan jumlah rak: 27 rak x 9 komik/rak = 243 komik. Ups, kok bukan 81? Tenang, ini sengaja dibuat lebih kompleks. Jika kita ubah soalnya menjadi: “Sebuah toko buku memiliki 9 rak, dan setiap rak berisi 9 komik. Berapa total komiknya?”. Maka penyelesaiannya menjadi 9 rak x 9 komik/rak = 81 komik. Perkalian 9 x 9 = 81 kembali digunakan untuk menghitung total komik di toko buku tersebut.

Perkalian 81 dalam Berbagai Sistem Bilangan

Angka 81, angka yang familiar dalam kehidupan sehari-hari, ternyata menyimpan misteri yang menarik jika kita menjelajahinya di luar sistem desimal yang biasa kita gunakan. Bayangkan, angka yang sama bisa direpresentasikan secara berbeda dalam sistem bilangan biner (basis 2) dan heksadesimal (basis 16)! Yuk, kita bongkar rahasia di balik transformasi angka 81 ini.

Konversi Bilangan 81 ke Sistem Biner

Sistem biner hanya menggunakan dua digit, 0 dan 1. Untuk mengubah 81 ke biner, kita perlu melakukan pembagian berulang dengan 2 sampai hasil bagi menjadi 0. Sisa pembagian dari setiap langkah, dibaca dari bawah ke atas, akan membentuk representasi binernya. Contohnya, 81 dibagi 2 menghasilkan 40 sisa 1, 40 dibagi 2 menghasilkan 20 sisa 0, dan seterusnya. Proses ini akan menghasilkan angka biner 1010001.

Konversi Bilangan 81 ke Sistem Heksadesimal

Sistem heksadesimal menggunakan 16 digit, dari 0 sampai 9 dan huruf A sampai F (A=10, B=11, C=12, D=13, E=14, F=15). Konversi ke heksadesimal bisa dilakukan dengan pembagian berulang dengan 16. Mirip dengan konversi biner, sisa pembagian dibaca dari bawah ke atas. Hasil konversi 81 ke heksadesimal adalah 51.

Proses Konversi Bilangan ke Sistem Biner dan Heksadesimal

Secara umum, konversi ke sistem bilangan lain melibatkan pembagian berulang dengan basis sistem bilangan target. Sisa pembagian, yang dibaca dari bawah ke atas, membentuk representasi bilangan dalam sistem bilangan tersebut. Perlu diingat, untuk sistem heksadesimal, sisa pembagian yang lebih besar dari 9 direpresentasikan dengan huruf A sampai F.

Representasi Bilangan 81 dalam Berbagai Sistem Bilangan

Sistem Bilangan	Representasi 81
Desimal	81
Biner	1010001
Heksadesimal	51

Contoh Konversi Bilangan Lain

Mari kita coba konversi bilangan lain, misalnya 255. Dalam sistem biner, 255 akan menjadi 11111111. Sementara dalam sistem heksadesimal, 255 akan menjadi FF. Proses konversi tetap sama, yaitu pembagian berulang dengan basis sistem bilangan target.

Pola Bilangan yang Menghasilkan 81

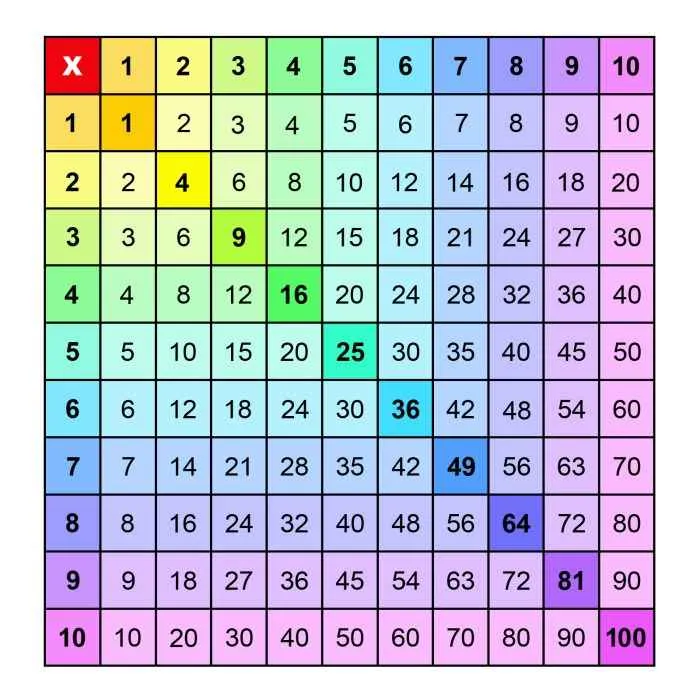
Angka 81, selain dikenal sebagai kuadrat dari 9, ternyata menyimpan segudang rahasia dalam bentuk pola bilangan perkalian. Kita akan mengungkap beberapa pola unik yang menghasilkan angka ajaib ini, lengkap dengan ilustrasi dan rumusnya. Siap-siap terpukau!

Lima Pola Bilangan Perkalian yang Menghasilkan 81

Berikut lima pola bilangan berbeda yang, jika dikalikan, menghasilkan 81. Setiap pola akan dijelaskan secara detail, termasuk contoh-contoh variasi dan ilustrasinya.

1. Pola 1: Perkalian Angka Sama: Pola paling sederhana adalah perkalian angka yang sama. 9 x 9 = 81. Ini adalah pola geometri dengan rasio 1. Ilustrasi: Sebuah persegi dengan sisi 9 satuan, luasnya merepresentasikan hasil perkalian 9 x 9 = 81 satuan persegi. Contoh lain: 3 x 3 = 9, 1 x 1 = 1, 12 x 12 = 144. Rumus: x * x = y, dimana x adalah angka yang dikalikan dan y adalah hasil perkalian.
2. Pola 2: Faktor-faktor 81: Pola ini menggunakan faktor-faktor dari 81. Contohnya, 3 x 27 = 81. Ilustrasi: Dua persegi panjang, satu dengan panjang 3 satuan dan lebar 27 satuan, dan yang lain dengan panjang 27 satuan dan lebar 3 satuan, keduanya memiliki luas 81 satuan persegi. Contoh lain: 1 x 81 = 81, 2 x 40.5 (bukan bilangan bulat), 4 x 20.25 (bukan bilangan bulat). Rumus: a * b = 81, dimana a dan b adalah faktor-faktor dari 81.
3. Pola 3: Pola Geometri dengan Rasio 3: 1 x 3 x 9 = 27. Kita bisa modifikasi dengan menambahkan angka 3 agar hasilnya 81. 1 x 3 x 9 x 3 = 81. Ilustrasi: Tiga kubus dengan ukuran sisi 1, 3, dan 9 satuan. Volume gabungan kubus tersebut direpresentasikan sebagai perkalian 1 x 3 x 9. Untuk mencapai 81, kita perlu menambahkan satu lagi faktor 3. Contoh lain: 2 x 6 x 18 = 216, 4 x 12 x 36 = 1728, 5 x 15 x 45 = 3375. Rumus: a x (3a) x (9a) x 3 = y, dimana a adalah angka awal dan y adalah hasil perkalian.
4. Pola 4: Kombinasi Faktor: Kita bisa menggunakan kombinasi faktor-faktor 81 secara kreatif. Misalnya, (3 x 3) x 9 = 81. Ilustrasi: Tiga persegi kecil dengan sisi 3 satuan disusun membentuk persegi besar dengan sisi 9 satuan. Luas persegi besar adalah 81 satuan persegi. Contoh lain: (2 x 2) x 20.25 = 81 (bukan bilangan bulat), (4 x 4) x 5.0625 = 81 (bukan bilangan bulat), (6 x 6) x 2.25 = 81. Rumus: (a x a) x b = 81, dimana a dan b adalah faktor-faktor dari 81.
5. Pola 5: Penggunaan Pangkat: 3⁴ = 81. Ilustrasi: Kubus dengan sisi 3 satuan, dengan volume 27 satuan kubik, kemudian dikalikan dengan 3 satuan untuk mencapai 81. Contoh lain: 2⁶ = 64, 4³ = 64, 5² = 25. Rumus: xⁿ = y, dimana x adalah basis, n adalah pangkat, dan y adalah hasil perkalian.

Tabel Perbandingan Pola

Berikut tabel perbandingan kelima pola bilangan yang telah dibahas:

Nama Pola	Deskripsi Singkat	Rumus	Contoh 1 (Hasil 81)	Contoh 2 (Hasil ≠ 81)
Perkalian Angka Sama	Perkalian angka yang sama	x * x = y	9 x 9 = 81	3 x 3 = 9
Faktor-faktor 81	Perkalian faktor-faktor 81	a * b = 81	3 x 27 = 81	1 x 81 = 81
Pola Geometri (Rasio 3)	Pola geometri dengan rasio 3	a x (3a) x (9a) x 3 = y	1 x 3 x 9 x 3 = 81	2 x 6 x 18 x 3 = 648
Kombinasi Faktor	Kombinasi faktor-faktor 81	(a x a) x b = 81	(3 x 3) x 9 = 81	(2 x 2) x 20.25 = 81
Penggunaan Pangkat	Menggunakan operasi pangkat	xn = y	34 = 81	26 = 64

Hubungan 81 dengan Bilangan Prima

Angka 81, kelihatannya sederhana, tapi menyimpan rahasia menarik terkait bilangan prima. Kita akan menguak misteri di balik angka ini, mengungkap bagaimana ia terhubung dengan blok bangunan matematika fundamental—bilangan prima. Siap-siap, perjalanan kita akan melibatkan faktorisasi prima, pohon faktor, dan bahkan sedikit pemrograman!

Faktorisasi Prima 81

Faktorisasi prima adalah proses memecah suatu bilangan bulat menjadi perkalian dari bilangan-bilangan prima. Bilangan prima sendiri adalah bilangan bulat lebih besar dari 1 yang hanya habis dibagi oleh 1 dan dirinya sendiri. Untuk 81, kita bisa melakukannya dengan langkah-langkah berikut:

1. 81 habis dibagi 3, hasilnya 27. Jadi, 81 = 3 x 27.
2. 27 juga habis dibagi 3, hasilnya 9. Maka, 81 = 3 x 3 x 9.
3. 9 juga habis dibagi 3, hasilnya 3. Sehingga, 81 = 3 x 3 x 3 x 3.

Karena 3 adalah bilangan prima (hanya habis dibagi 1 dan 3), maka faktorisasi prima dari 81 adalah 3 x 3 x 3 x 3 atau 3⁴. Ini menunjukkan bahwa 81 dibangun dari perkalian berulang bilangan prima 3.

Hubungan Faktorisasi Prima dengan Perkalian

Faktorisasi prima menunjukkan bagaimana suatu bilangan dapat dibangun dari perkalian bilangan prima. Persamaan matematika 81 = 3 x 3 x 3 x 3 menunjukkan hubungan langsung antara faktorisasi prima (3) dan bilangan itu sendiri (81). Contoh lain, misalnya 12 = 2 x 2 x 3, di mana 2 dan 3 adalah faktor prima dari 12.

Pohon Faktor Bilangan 81

Berikut ilustrasi pohon faktor untuk 81:

81
/ \
3 27
/ \
3 9
/ \
3 3

Pohon faktor ini secara visual menunjukkan bagaimana 81 diuraikan menjadi faktor-faktornya hingga mencapai faktor prima (3).

Konsep Faktorisasi Prima, Perkalian yang hasilnya 81

Faktorisasi prima adalah proses penguraian suatu bilangan komposit (bilangan yang bukan prima) menjadi perkalian dari bilangan-bilangan prima. Faktor prima adalah bilangan prima yang membagi habis suatu bilangan. Bilangan prima itu sendiri tidak dapat difaktorisasi lebih lanjut, contohnya 7, 11, 13 dan seterusnya.

Contoh Faktorisasi Prima untuk Bilangan Lain

Berikut beberapa contoh faktorisasi prima untuk bilangan lain:

Bilangan	Faktorisasi Prima	Langkah-langkah Faktorisasi
24	23 x 3	24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3
35	5 x 7	35 = 5 x 7 (keduanya prima)
100	22 x 52	100 = 2 x 50 = 2 x 2 x 25 = 2 x 2 x 5 x 5

Kesimpulan Hubungan 81 dan Bilangan Prima

81 hanya terdiri dari faktor prima 3, menunjukkan ketergantungan penuh pada bilangan prima ini dalam pembentukannya.

81 sebagai Bilangan Kuadrat Sempurna

Ya, 81 adalah bilangan kuadrat sempurna karena 81 = 9². Hubungannya dengan faktorisasi prima adalah bahwa pangkat 4 dari 3 (3⁴) dapat disederhanakan menjadi (3²)² = 9².

Perbandingan Faktorisasi Prima 81 dan 80

Faktorisasi prima 81 adalah 3⁴, sementara faktorisasi prima 80 adalah 2⁴ x 5. Keduanya memiliki pangkat 4, tetapi basisnya berbeda. 81 hanya memiliki faktor prima 3, sedangkan 80 memiliki faktor prima 2 dan 5.

Program Faktorisasi Prima

Berikut pseudocode untuk program faktorisasi prima:

fungsi faktorisasiPrima(n):
  jika n <= 1:
    kembalikan [] // Bilangan kurang dari atau sama dengan 1 bukan prima
  faktor = []
  i = 2
  sementara i * i <= n:
    sementara n % i == 0:
      tambahkan i ke faktor
      n = n / i
    i = i + 1
  jika n > 1:
    tambahkan n ke faktor
  kembalikan faktor

// Contoh penggunaan:
bilangan = 81
faktor = faktorisasiPrima(bilangan)
cetak "Faktor prima dari", bilangan, "adalah:", faktor

Perkalian 81 dan Sifat-Sifat Bilangan

Angka 81, selain dikenal sebagai kuadrat dari 9, juga menyimpan rahasia menarik dalam dunia perkalian. Lebih dari sekadar hasil perkalian 9 x 9, angka ini menjadi lahan subur untuk memahami sifat-sifat bilangan yang mendasari operasi perkalian. Mari kita telusuri lebih dalam!

Sifat Komutatif Perkalian

Sifat komutatif dalam perkalian menyatakan bahwa urutan perkalian tidak mempengaruhi hasil akhirnya. Dengan kata lain, a x b = b x a. Ini berlaku juga untuk angka 81. Kita bisa mendapatkan 81 dengan berbagai kombinasi perkalian, misalnya 9 x 9, atau 1 x 81, atau bahkan 3 x 27. Hasilnya tetap sama, yaitu 81, meskipun urutan angka yang dikalikan berbeda.

• 9 x 9 = 81
• 1 x 81 = 81
• 3 x 27 = 81
• 27 x 3 = 81

Sifat ini memudahkan kita dalam melakukan perhitungan, karena kita bisa memilih urutan perkalian yang paling mudah dihitung.

Sifat Asosiatif Perkalian

Sifat asosiatif menjelaskan bahwa ketika kita mengalikan lebih dari dua bilangan, pengelompokan bilangan tersebut tidak akan mengubah hasil akhir. Rumusnya adalah (a x b) x c = a x (b x c). Bayangkan kita ingin menghitung 3 x 3 x 9. Kita bisa mengelompokkannya sebagai (3 x 3) x 9 = 9 x 9 = 81, atau 3 x (3 x 9) = 3 x 27 = 81. Hasilnya tetap 81!

• (3 x 3) x 9 = 81
• 3 x (3 x 9) = 81

Kegunaan sifat ini terlihat jelas saat berhadapan dengan perkalian bilangan yang lebih kompleks, mempermudah perhitungan bertahap.

Penerapan Sifat-Sifat Bilangan dalam Perkalian Lain

Sifat komutatif dan asosiatif bukan hanya berlaku untuk perkalian yang menghasilkan 81. Kedua sifat ini merupakan prinsip dasar dalam aljabar dan matematika secara umum. Contohnya, dalam menghitung luas persegi panjang dengan panjang 12 cm dan lebar 7 cm, kita bisa menggunakan sifat komutatif: 12 cm x 7 cm = 7 cm x 12 cm = 84 cm². Atau, dalam menghitung volume balok dengan ukuran 2 cm x 3 cm x 4 cm, sifat asosiatif membantu: (2 x 3) x 4 cm³ = 2 x (3 x 4) cm³ = 24 cm³.

Memahami sifat-sifat ini memungkinkan kita untuk melakukan perhitungan dengan lebih efisien dan akurat, terutama dalam situasi yang melibatkan angka-angka yang lebih besar dan kompleks.

Representasi Geometris Perkalian 81: Perkalian Yang Hasilnya 81

Perkalian, selain sekadar angka-angka yang dikalikan, bisa juga divisualisasikan secara geometris! Bayangkan angka-angka itu membentuk bentuk-bentuk nyata yang bisa kita lihat dan pahami. Ini bikin belajar perkalian jadi lebih seru dan nggak cuma menghafal rumus doang, kan? Nah, kali ini kita bakal bahas bagaimana angka 81 bisa direpresentasikan secara geometris, khususnya lewat bentuk-bentuk persegi dan persegi panjang.

Luas Persegi sebagai Representasi Perkalian 81

Salah satu representasi geometris paling sederhana untuk 81 adalah luas persegi. Karena 9 x 9 = 81, kita bisa membayangkan sebuah persegi dengan sisi sepanjang 9 satuan. Luas persegi ini, yang dihitung dengan mengalikan panjang sisi dengan panjang sisi (sisi x sisi), akan tepat 81 satuan luas. Coba bayangkan persegi itu terbagi menjadi 81 kotak kecil berukuran 1×1 satuan. Setiap kotak kecil mewakili satu satuan luas, dan totalnya ada 81 kotak, mewakili hasil perkalian 9 x 9.

Representasi Geometris Perkalian Lain

Selain persegi, ada banyak cara lain untuk merepresentasikan perkalian yang menghasilkan 81 secara geometris. Kita bisa menggunakan persegi panjang. Misalnya, persegi panjang dengan panjang 27 satuan dan lebar 3 satuan juga memiliki luas 81 satuan (27 x 3 = 81). Atau, kita bisa menggunakan kombinasi bentuk geometris lainnya, asalkan total luasnya 81 satuan. Kreativitasmu di sini diuji!

Detail Representasi Geometris Persegi 9×9

Mari kita kembali ke persegi 9×9. Bayangkan persegi itu terbagi menjadi sembilan baris dan sembilan kolom, masing-masing berisi sembilan kotak kecil. Setiap baris mewakili perkalian 9 x 1, dan setiap kolom mewakili perkalian 1 x 9. Dengan menghitung total kotak kecil (9 baris x 9 kolom), kita mendapatkan total luas 81 satuan. Ini menunjukkan secara visual bagaimana perkalian 9 x 9 menghasilkan 81.

Manfaat Representasi Geometris dalam Memahami Perkalian

Representasi geometris membantu kita memahami konsep perkalian secara lebih intuitif. Dengan melihat bentuk-bentuk geometris, kita tidak hanya menghafal hasil perkalian, tetapi juga memahami *proses* perkalian itu sendiri. Ini khususnya berguna untuk anak-anak yang masih belajar perkalian, karena visualisasi membantu mereka menghubungkan angka-angka abstrak dengan sesuatu yang konkret dan mudah dipahami. Mereka bisa benar-benar *melihat* bagaimana angka-angka itu saling berinteraksi untuk menghasilkan hasil akhir.

Perkalian 81 dalam Konteks Algoritma

Angka 81, selain dikenal sebagai kuadrat dari 9, juga menyimpan potensi menarik dalam dunia algoritma. Kita bisa mengeksplorasi berbagai cara untuk menghasilkan angka ini melalui perkalian, dan prosesnya itu sendiri bisa diuraikan dalam bentuk algoritma yang sederhana dan mudah dipahami. Dengan memahami algoritma ini, kita nggak cuma bisa menghitung perkalian dengan hasil 81, tapi juga bisa memodifikasinya untuk menghasilkan perkalian dengan hasil yang berbeda. Bayangkan, kayak membangun sebuah mesin hitung mini yang bisa kita atur sendiri!

Algoritma Sederhana untuk Menghasilkan Perkalian dengan Hasil 81

Algoritma berikut ini akan menghasilkan perkalian dengan hasil 81. Algoritma ini dirancang untuk fleksibel, sehingga kita bisa dengan mudah memodifikasinya untuk menghasilkan perkalian dengan hasil yang berbeda. Ini akan melibatkan penentuan faktor-faktor yang akan dikalikan, dan algoritma akan memastikan hasil perkaliannya selalu 81.

Langkah-langkah Algoritma

1. Tentukan dua angka (faktor) yang jika dikalikan menghasilkan 81. Contohnya, 9 dan 9, atau 3 dan 27, atau 1 dan 81.
2. Simpan kedua angka tersebut dalam variabel, misalnya variabel faktor1 dan faktor2.
3. Kalikan kedua variabel tersebut (faktor1 * faktor2).
4. Tampilkan hasilnya. Jika hasilnya 81, maka algoritma berhasil. Jika tidak, periksa kembali angka yang digunakan.

Pseudocode Algoritma

Berikut pseudocode yang merepresentasikan algoritma di atas:


BEGIN
faktor1 ← 9
faktor2 ← 9
hasil ← faktor1 * faktor2
PRINT hasil // Output: 81
END


Contoh Penerapan Algoritma

Misalnya, kita ingin menggunakan faktor 3 dan 27. Algoritma akan berjalan seperti ini:

1. faktor1 diinisialisasi dengan nilai 3.
2. faktor2 diinisialisasi dengan nilai 27.
3. hasil akan menjadi 3 * 27 = 81.
4. Algoritma menampilkan 81.

Modifikasi Algoritma untuk Hasil Perkalian yang Berbeda

Modifikasi algoritma ini sangat mudah. Cukup ubah nilai faktor1 dan faktor2 dengan angka-angka yang jika dikalikan menghasilkan angka yang diinginkan. Misalnya, untuk menghasilkan perkalian dengan hasil 100, kita bisa mengubah nilai faktor1 menjadi 10 dan faktor2 menjadi 10. Atau, kita bisa menggunakan faktor-faktor lain seperti 25 dan 4, atau 20 dan 5. Intinya, fleksibilitas algoritma ini terletak pada kemampuannya untuk beradaptasi dengan angka-angka yang berbeda.

Perbandingan Berbagai Metode Perkalian Menuju 81

Mendapatkan angka 81 lewat perkalian ternyata bisa dilakukan dengan berbagai cara, lho! Dari metode yang sederhana sampai yang sedikit lebih rumit, semuanya punya kelebihan dan kekurangan masing-masing. Nah, kali ini kita akan membandingkan beberapa metode perkalian untuk mencapai angka 81, dengan fokus pada efisiensi dan kemudahan pemahamannya. Siap-siap terkejut dengan perbedaannya!

Metode Perkalian dan Perbandingannya

Berikut perbandingan lima metode perkalian yang berbeda untuk mencapai hasil 81. Kita akan melihat contoh perhitungan, kelebihan, kekurangan, jumlah langkah, dan tingkat kemudahan pemahamannya.

Metode Perkalian	Contoh Perhitungan	Kelebihan	Kekurangan	Jumlah Langkah	Kemudahan Pemahaman (1-5)
Perkalian Langsung	9 x 9 = 81	Cepat dan mudah jika sudah menghafal perkalian 9	Tidak efektif jika belum menghafal perkalian 9	1	5
Perkalian Bersusun	9 x 9 — 81	Sistematis dan mudah dipahami, cocok untuk angka yang lebih besar	Lebih banyak langkah dibandingkan perkalian langsung	3	4
Perkalian dengan Sifat Distributif	(10-1) x (10-1) = 100 – 20 + 1 = 81 atau (5 x 3) x (3 x 3 x 3) = 15 x 27 = 81 (kurang efisien untuk 81)	Memudahkan perhitungan jika angka bisa didekomposisi menjadi angka yang lebih mudah dikalikan	Membutuhkan pemahaman yang lebih mendalam tentang sifat distributif dan bisa jadi lebih rumit untuk beberapa angka	3-4	3
Perkalian dengan Faktorisasi Prima	81 = 3 x 3 x 3 x 3 = 34	Menunjukkan faktor-faktor pembentuk angka, berguna dalam memahami sifat angka	Tidak efisien untuk perhitungan langsung, lebih cocok untuk analisis angka	Variabel, tergantung kompleksitas faktorisasi	2
Perkalian Menggunakan Bilangan Berpangkat	92 = 81 atau 34 = 81	Singkat dan efisien jika sudah memahami konsep bilangan berpangkat	Membutuhkan pemahaman konsep bilangan berpangkat	1	3

Kriteria Penentuan Efisiensi Metode Perkalian

Efisiensi metode perkalian ditentukan berdasarkan tiga kriteria utama: jumlah langkah perhitungan, kemudahan pemahaman, dan potensi kesalahan. Jumlah langkah dihitung secara langsung dari proses perhitungan. Kemudahan pemahaman dinilai dengan skala 1-5 (5 paling mudah), berdasarkan seberapa mudah metode tersebut dipahami dan diterapkan oleh seseorang yang memiliki pengetahuan matematika dasar. Potensi kesalahan dipertimbangkan secara kualitatif, yaitu seberapa besar kemungkinan terjadinya kesalahan hitung pada setiap metode.

Visualisasi Metode Perkalian Paling Efisien

Berdasarkan tabel di atas, metode perkalian langsung (9 x 9 = 81) merupakan metode paling efisien untuk mendapatkan angka 81. Ini karena memiliki jumlah langkah paling sedikit (hanya satu langkah) dan tingkat kemudahan pemahaman yang tertinggi (skala 5). Visualisasinya sangat sederhana: dua buah persegi dengan sisi 9 satuan dikalikan menghasilkan luas persegi sebesar 81 satuan.

Efisiensi Metode Perkalian untuk Angka Lain

Efisiensi metode-metode tersebut akan berubah jika angka yang ingin dicapai berbeda. Untuk angka yang lebih besar seperti 144 (12 x 12), perkalian bersusun mungkin menjadi lebih efisien daripada perkalian langsung karena menghafal perkalian 12 mungkin lebih sulit. Sedangkan untuk angka yang lebih kecil seperti 25 (5 x 5), perkalian langsung tetap menjadi yang paling efisien.

Ulasan Penutup

Ternyata, angka 81 lebih dari sekadar hasil perkalian 9 x 9! Perjalanan kita mengeksplorasi berbagai metode untuk mendapatkan angka 81 telah membuka mata kita terhadap keindahan dan kompleksitas matematika. Dari faktorisasi prima hingga representasi geometris, setiap pendekatan memberikan pemahaman yang lebih dalam tentang konsep perkalian dan sifat-sifat bilangan. Jadi, jangan pernah meremehkan angka sederhana, karena di balik kesederhanaannya tersimpan keajaiban matematika yang tak terbatas!