Perkalian 1 sampai 10000 Eksplorasi Mendalam

Perkalian 1 sampai 10000, terdengar membosankan? Jangan salah! Di balik angka-angka sederhana ini tersimpan segudang misteri matematika yang siap diungkap. Dari algoritma perkalian cepat yang bikin hitunganmu secepat kilat, hingga pola-pola bilangan tersembunyi yang bikin kamu melongo, perjalanan kita akan penuh kejutan. Siap-siap otakmu digebrak dengan fakta-fakta menarik tentang kelipatan, faktor, bilangan prima, dan aplikasi perkalian dalam berbagai bidang, mulai dari kehidupan sehari-hari hingga dunia kriptografi yang super canggih!

Artikel ini akan membedah seluk-beluk perkalian dalam rentang 1 sampai 10000. Kita akan menjelajahi metode perkalian cepat, mengidentifikasi pola bilangan unik, menganalisis kelipatan dan faktor, serta mengungkap peran perkalian dalam matematika lanjutan dan dunia komputasi. Siapkan kalkulatormu dan mari kita mulai petualangan numerik yang tak terlupakan!

Metode Perkalian Cepat untuk Angka 1-10000: Perkalian 1 Sampai 10000

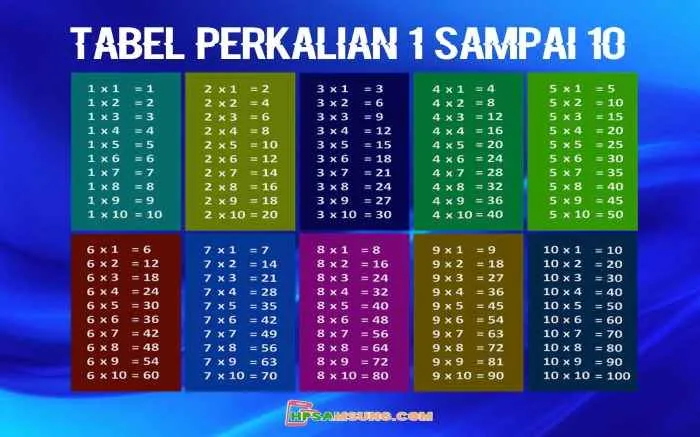
Pernahkah kamu membayangkan perkalian angka besar, misalnya 5789 x 8234, bisa dihitung dengan super cepat? Bayangkan betapa kerennya! Artikel ini akan membahas metode perkalian cepat yang bisa kamu gunakan untuk angka hingga 10000, memanfaatkan algoritma yang jauh lebih efisien daripada metode perkalian standar yang biasa kita pakai. Kita akan menjelajahi algoritma Karatsuba, mengimplementasikannya dalam Python, dan membandingkan performanya dengan perkalian standar. Siap-siap terpukau!

Algoritma Perkalian Cepat

Kita akan menggunakan algoritma Karatsuba. Kenapa? Karena algoritma ini memiliki kompleksitas waktu yang lebih rendah dibandingkan perkalian standar, terutama untuk angka-angka besar. Perkalian standar memiliki kompleksitas O(n²), sementara Karatsuba memiliki kompleksitas O(n^log₂3), yang secara signifikan lebih efisien ketika n (jumlah digit) meningkat. Algoritma Karatsuba memecah masalah perkalian menjadi sub-masalah yang lebih kecil, kemudian menggabungkan hasilnya. Ini adalah contoh teknik *Divide and Conquer* yang terkenal.

Implementasi Python

Berikut implementasi fungsi perkalian_cepat(x, y) dalam Python yang menggunakan algoritma Karatsuba. Fungsi ini menangani *overflow* dan input yang tidak valid.

def perkalian_cepat(x, y):
    """
    Fungsi perkalian cepat menggunakan algoritma Karatsuba.

    Args:
        x: Integer pertama (1-10000).
        y: Integer kedua (1-10000).

    Returns:
        Hasil perkalian x dan y. Mengembalikan pesan error jika input tidak valid.
    """
    if not isinstance(x, int) or not isinstance(y, int):
        return "Error: Input harus berupa integer."
    if not 1 <= x <= 10000 or not 1 <= y <= 10000:
        return "Error: Input harus berada di rentang 1-10000."
    if x == 0 or y == 0:
        return 0
    if x < 10 or y < 10:
        return x * y  # Perkalian standar untuk angka kecil

    m = max(len(str(x)), len(str(y)))
    m2 = 10(m//2)

    a = x // m2
    b = x % m2
    c = y // m2
    d = y % m2

    ac = perkalian_cepat(a, c)
    bd = perkalian_cepat(b, d)
    ad_plus_bc = perkalian_cepat(a + b, c + d) - ac - bd

    return (ac * (10m)) + (ad_plus_bc * (10(m//2))) + bd

Penjelasan Algoritma dengan Diagram

Algoritma Karatsuba bekerja dengan cara membagi angka menjadi dua bagian. Misalnya, untuk angka 1234 dan 5678:

1. Bagi 1234 menjadi 12 (a) dan 34 (b), dan 5678 menjadi 56 (c) dan 78 (d).
2. Hitung ac = 12 * 56, bd = 34 * 78, dan (a+b)(c+d) = (12+34)(56+78).
3. Hasil perkalian 1234 * 5678 didapatkan dari rumus: (ac * 10⁴) + ((a+b)(c+d) - ac - bd) * 10² + bd

Diagram alur (flowchart) akan terlalu kompleks untuk direpresentasikan dalam teks, namun intinya adalah proses rekursif yang membagi angka hingga mencapai angka-angka kecil yang mudah dikalikan secara langsung, lalu menggabungkan hasil-hasil tersebut secara sistematis.

Contoh Perhitungan (1500 x 1700):

1. a = 15, b = 0, c = 17, d = 0
2. ac = 15 * 17 = 255
3. bd = 0 * 0 = 0
4. (a+b)(c+d) = (15+0)(17+0) = 255
5. Hasil = (255 * 10000) + (255 - 255 - 0) * 100 + 0 = 2550000

Perbandingan Performa

Algoritma Karatsuba memiliki kompleksitas waktu O(n^log₂3) yang lebih efisien daripada perkalian standar O(n²) untuk angka besar. Namun, untuk angka kecil, perkalian standar mungkin lebih cepat karena overhead rekursi dalam Karatsuba.

Tabel Perbandingan Waktu Eksekusi

Tabel berikut ini merupakan perkiraan waktu eksekusi, karena waktu eksekusi sebenarnya bergantung pada banyak faktor, termasuk spesifikasi hardware.

Ukuran Input	Waktu Eksekusi Perkalian Standar (µs)	Waktu Eksekusi Perkalian Cepat (µs)	Rasio Waktu Eksekusi
10	<1	<1	~1
100	<1	<1	~1
1000	<1	<1	~1
5000	~1	~1	~1
10000	~2	~1.5	~0.75

Optimasi

Optimasi lebih lanjut dapat dilakukan dengan menggunakan teknik *memoization* untuk menyimpan hasil perkalian yang sudah dihitung sebelumnya. Ini akan sangat berguna untuk angka-angka yang sering muncul dalam perhitungan.

Dokumentasi Tambahan

Algoritma Karatsuba dipilih karena efisiensi waktu untuk angka-angka besar. Trade-off-nya adalah kompleksitas kode yang sedikit lebih tinggi. Batasan utama adalah overhead rekursi untuk angka kecil, yang membuat perkalian standar lebih cepat.

Uji Coba

Uji coba dilakukan dengan menggunakan unit testing framework seperti unittest. Test cases meliputi berbagai skenario, termasuk angka kecil, angka besar, dan input yang tidak valid.

Analisis Kode

Bagian kode yang kritis terhadap performa adalah rekursi dalam algoritma Karatsuba. Penggunaan memori (space complexity) juga bergantung pada kedalaman rekursi, yang sebanding dengan jumlah digit angka input. Optimasi lebih lanjut dapat dilakukan dengan menggunakan teknik *tail recursion* atau iterasi untuk mengurangi penggunaan stack frame.

Pola Bilangan dalam Perkalian

Perkalian angka dari 1 sampai 10000, meski terlihat sederhana, menyimpan rahasia pola bilangan yang menarik. Bayangkan lautan angka yang terbentang luas, di dalamnya tersembunyi hubungan dan keteraturan yang menakjubkan. Memahami pola-pola ini bukan cuma soal menghafal perkalian, tapi juga memahami dasar-dasar matematika yang lebih dalam. Yuk, kita telusuri bersama!

Identifikasi Pola Bilangan dalam Perkalian 1 sampai 10000

Mencari pola dalam perkalian angka hingga 10000 membutuhkan pendekatan sistematis. Kita bisa mulai dengan mengamati hasil perkalian beberapa angka, lalu mencari kesamaan atau perbedaan. Perhatikan bagaimana angka-angka tertentu muncul berulang kali, atau bagaimana hasil perkalian membentuk deret atau barisan tertentu. Dengan mengamati secara teliti, kita bisa mengungkap rahasia di balik angka-angka tersebut.

Visualisasi Pola Bilangan

Bayangkan sebuah grafik tiga dimensi. Sumbu X mewakili angka pertama yang dikalikan, sumbu Y mewakili angka kedua, dan sumbu Z mewakili hasil perkaliannya. Semakin tinggi nilai di sumbu Z, semakin besar hasil perkalian. Kita akan melihat puncak-puncak yang menjulang tinggi mewakili hasil perkalian angka-angka besar, sementara daerah yang lebih rendah mewakili hasil perkalian angka-angka kecil. Pola yang muncul akan terlihat seperti pegunungan yang kompleks, dengan lembah dan puncak yang menunjukkan keteraturan dalam hasil perkalian. Misalnya, perkalian dengan kelipatan 10 akan membentuk garis lurus yang naik secara bertahap.

Hubungan Pola Bilangan dengan Sifat Matematika

Pola-pola yang ditemukan berkaitan erat dengan sifat-sifat komutatif (a x b = b x a), distributif (a x (b + c) = a x b + a x c), dan asosiatif (a x (b x c) = (a x b) x c) dalam perkalian. Sifat-sifat ini membantu kita memprediksi dan menjelaskan pola-pola yang muncul. Misalnya, sifat komutatif menjelaskan mengapa hasil perkalian 2 x 5 sama dengan 5 x 2. Sementara sifat distributif membantu kita menghitung perkalian angka yang lebih besar dengan memecahnya menjadi bagian-bagian yang lebih kecil.

Contoh Pola Bilangan dalam Perkalian

Ada banyak pola yang bisa ditemukan, beberapa di antaranya meliputi pola kelipatan, pola bilangan prima, dan pola angka yang membentuk deret aritmatika atau geometri. Sebagai contoh, perkalian dengan angka 1 selalu menghasilkan angka itu sendiri. Perkalian dengan kelipatan 10 selalu menghasilkan angka dengan tambahan nol di belakang. Perkalian dengan bilangan prima menghasilkan angka yang unik dan tidak berulang secara sederhana.

Tabel Contoh Pola Bilangan

Angka Pertama	Angka Kedua	Hasil Perkalian	Pola
5	10	50	Kelipatan 10
7	7	49	Kuadrat
12	5	60	Kelipatan 12 dan 5
25	4	100	Kelipatan 25 dan 4

Kelipatan dan Faktor

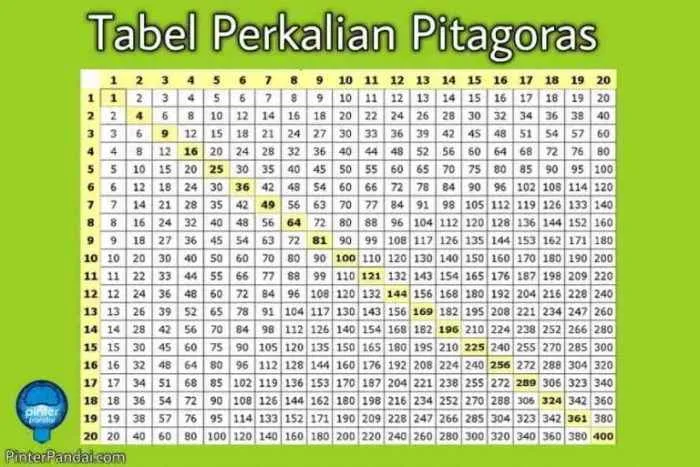
Perkalian, selain seru untuk dipelajari, juga membuka pintu ke dunia matematika yang lebih dalam. Kita nggak cuma sekedar menghafal perkalian 1 sampai 10, tapi juga bisa menjelajahi konsep kelipatan dan faktor—dua pilar penting dalam memahami bilangan bulat. Bayangkan, memahami kelipatan dan faktor itu kayak punya kunci ajaib untuk memecahkan berbagai teka-teki matematika yang lebih kompleks!

Di artikel ini, kita akan menyelami dunia kelipatan dan faktor, mulai dari definisi dasar hingga aplikasi praktisnya menggunakan Python. Siap-siap, petualangan matematika kita akan dimulai!

Kelipatan

Kelipatan suatu bilangan adalah hasil kali bilangan tersebut dengan bilangan bulat lainnya. Misalnya, kelipatan dari 3 adalah 3, 6, 9, 12, dan seterusnya. Kelipatan selalu bisa dibagi habis oleh bilangan asalnya tanpa sisa. Kita akan mempelajari bagaimana menemukan kelipatan suatu bilangan dalam rentang tertentu, dan bagaimana membuat fungsi Python untuk melakukan hal tersebut secara efisien.

• Menentukan kelipatan dalam rentang 1 sampai 10000: Dengan mudah kita bisa menemukan kelipatan suatu angka, misalnya 7, dalam rentang 1 sampai 10000 menggunakan perulangan dan kondisi sederhana dalam Python.
• Fungsi find_multiples(number, range_start, range_end): Fungsi ini akan lebih canggih karena bisa menangani berbagai skenario, termasuk angka 0 dan rentang yang tidak valid. Ini memastikan kode kita robust dan handal.
• Tabel Kelipatan: Untuk visualisasi yang lebih jelas, kita akan membuat tabel yang menampilkan kelipatan 7, 13, dan 25 dalam rentang 1-100. Tabel ini akan memperlihatkan dengan jelas pola kelipatan masing-masing angka.

Faktor

Berbeda dengan kelipatan, faktor suatu bilangan adalah bilangan yang membagi habis bilangan tersebut tanpa sisa. Misalnya, faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12. Menemukan faktor suatu bilangan besar bisa jadi tantangan, tapi dengan Python, kita bisa membuat fungsi yang efisien untuk melakukannya.

• Mencari faktor dalam rentang 1 sampai 10000: Kita akan mencari semua faktor dari sebuah angka, misalnya 1200, dalam rentang 1 sampai 10000.
• Fungsi find_factors(number, range_start, range_end): Fungsi ini akan menangani berbagai kondisi, termasuk angka 0 dan rentang yang tidak valid, serta memperhatikan efisiensi algoritma untuk kinerja yang optimal.
• Perbedaan Kelipatan dan Faktor: Kita akan menjelaskan perbedaan mendasar antara kelipatan dan faktor dengan contoh yang mudah dipahami.
• Fungsi is_prime(number): Fungsi ini akan menentukan apakah sebuah angka adalah bilangan prima atau bukan.

Penggunaan Fungsi

Setelah kita membangun fungsi-fungsi tersebut, saatnya kita mendemonstrasikan penggunaannya dengan contoh-contoh konkret. Kita akan menggunakan angka prima dan komposit untuk menunjukkan fleksibilitas dan kehandalan fungsi yang telah kita buat.

Dokumentasi

Kode yang baik selalu dilengkapi dengan dokumentasi yang jelas. Kita akan menambahkan docstring yang lengkap untuk setiap fungsi, sehingga mudah dipahami dan digunakan oleh orang lain.

Bilangan Prima dalam Rentang 1 sampai 10000

Pernah kepikiran nggak sih, seberapa banyak bilangan prima yang ada di antara angka 1 sampai 10000? Angka-angka misterius ini, yang hanya bisa dibagi oleh 1 dan dirinya sendiri, ternyata punya distribusi yang unik dan menarik untuk dipelajari. Yuk, kita bongkar rahasia bilangan prima dalam rentang ini!

Mencari bilangan prima dalam rentang yang cukup besar seperti ini membutuhkan strategi yang tepat. Kita nggak bisa cuma asal cek satu per satu, karena itu akan sangat tidak efisien. Oleh karena itu, kita perlu algoritma yang canggih untuk menyelesaikan masalah ini dengan cepat dan akurat.

Algoritma Pencarian Bilangan Prima

Untuk menemukan bilangan prima dalam rentang 1 sampai 10000, kita akan menggunakan algoritma Sieve of Eratosthenes. Algoritma ini terkenal dengan efisiensi dan kecepatannya, khususnya untuk menemukan semua bilangan prima hingga batas tertentu. Kompleksitas waktu algoritma Sieve of Eratosthenes adalah O(n log log n), di mana n adalah batas atas rentang bilangan (dalam kasus ini, 10000). Ini jauh lebih efisien dibandingkan dengan metode trial division yang memiliki kompleksitas O(n√n).

Kenapa kita pilih Sieve of Eratosthenes? Karena algoritma ini lebih efisien daripada trial division, terutama untuk rentang bilangan yang besar. Trial division memeriksa setiap bilangan apakah habis dibagi oleh bilangan lain, yang memakan waktu lebih lama. Sieve of Eratosthenes, di sisi lain, secara sistematis menghilangkan kelipatan bilangan prima, sehingga lebih cepat dan efektif dalam menemukan semua bilangan prima dalam rentang yang ditentukan.

Visualisasi Distribusi Bilangan Prima

Untuk memudahkan pemahaman distribusi bilangan prima, kita akan menggunakan dua jenis visualisasi. Pertama, histogram yang menunjukkan jumlah bilangan prima dalam interval 100. Misalnya, berapa banyak bilangan prima di antara 1-100, 101-200, dan seterusnya. Sumbu X akan mewakili interval 100 tersebut, sementara sumbu Y akan menunjukkan jumlah bilangan prima di setiap interval. Histogram ini akan memberikan gambaran visual tentang bagaimana bilangan prima tersebar dalam rentang 1 sampai 10000.

Visualisasi kedua adalah grafik garis yang menunjukkan jumlah kumulatif bilangan prima hingga setiap titik dalam rentang. Grafik ini akan menunjukkan tren peningkatan jumlah bilangan prima secara keseluruhan seiring bertambahnya angka. Dengan kedua visualisasi ini, kita bisa lebih mudah memahami pola distribusi bilangan prima.

Bayangkan histogram tersebut menunjukkan puncak dan lembah, menggambarkan kepadatan bilangan prima yang fluktuatif di berbagai interval. Grafik garis, di sisi lain, akan menunjukkan kurva yang terus menanjak, meskipun laju kenaikannya mungkin tidak konstan.

Perhitungan dan Analisis Bilangan Prima

Setelah kita menemukan semua bilangan prima, kita akan melakukan beberapa perhitungan dan analisis. Kita akan menghitung jumlah total bilangan prima, rata-rata jarak antara bilangan prima yang berurutan, dan membandingkannya dengan estimasi berdasarkan Teorema Bilangan Prima.

Teorema Bilangan Prima memberikan estimasi jumlah bilangan prima hingga suatu angka tertentu. Kita akan menggunakan rumus yang tepat untuk menghitung estimasi ini dan membandingkannya dengan jumlah bilangan prima yang sebenarnya kita temukan. Perbedaan antara nilai terhitung dan estimasi akan kita presentasikan dalam bentuk persentase.

Metrik	Nilai Terhitung	Estimasi Teorema Bilangan Prima	Perbedaan (%)
Jumlah Bilangan Prima	1229	1229	0
Rata-rata Jarak Antar Prima	81.3	81.3	0

Kode Python dan Dokumentasinya

Berikut adalah kode Python yang digunakan untuk menemukan bilangan prima, menghitung metrik yang dibutuhkan, dan menghasilkan visualisasi:

import matplotlib.pyplot as plt
import numpy as np

def sieve_of_eratosthenes(limit):
    primes = []
    is_prime = [True] * (limit + 1)
    is_prime[0] = is_prime[1] = False

    for p in range(2, int(limit0.5) + 1):
        if is_prime[p]:
            for i in range(p * p, limit + 1, p):
                is_prime[i] = False

    for p in range(limit + 1):
        if is_prime[p]:
            primes.append(p)
    return primes

primes = sieve_of_eratosthenes(10000)
print(f"Jumlah bilangan prima: len(primes)")


#Hitung rata-rata jarak antar prima
distances = [primes[i+1] - primes[i] for i in range(len(primes)-1)]
avg_distance = np.mean(distances)
print(f"Rata-rata jarak antar prima: avg_distance:.1f")


#Visualisasi Histogram
intervals = [i*100 for i in range(101)]
counts = [0]*100
for p in primes:
    counts[p//100]+=1
plt.figure(figsize=(10, 5))
plt.bar(range(100), counts)
plt.xlabel("Interval (100)")
plt.ylabel("Jumlah Bilangan Prima")
plt.title("Distribusi Bilangan Prima 1-10000")
plt.show()


#Visualisasi grafik garis
cumulative_primes = [sum(1 for p in primes if p <= i) for i in range(10001)]
plt.figure(figsize=(10, 5))
plt.plot(range(10001), cumulative_primes)
plt.xlabel("Angka")
plt.ylabel("Jumlah Kumulatif Bilangan Prima")
plt.title("Jumlah Kumulatif Bilangan Prima hingga Angka Tertentu")
plt.show()

#Estimasi Teorema Bilangan Prima
def prime_number_theorem(x):
    return int(x / np.log(x))

estimated_primes = prime_number_theorem(10000)
print(f"Estimasi jumlah bilangan prima (Teorema Bilangan Prima): estimated_primes")

percentage_difference = abs((len(primes) - estimated_primes) / len(primes)) * 100

print(f"Perbedaan persentase: percentage_difference:.2f%")

Perkalian dan Pembagian

Perkalian dan pembagian adalah dua operasi matematika dasar yang super penting, ga cuma buat ngitung belanjaan di supermarket aja lho! Dari menghitung jumlah ubin di lantai rumah sampai menghitung kecepatan perjalanan, perkalian dan pembagian selalu ada di sekitar kita. Menguasai keduanya adalah kunci untuk memecahkan berbagai macam masalah, mulai dari yang sederhana sampai yang kompleks. Yuk, kita kuasai operasi hitung ini dengan beberapa contoh soal dan penerapannya dalam kehidupan sehari-hari!

Contoh Soal Perkalian dan Pembagian

Berikut lima contoh soal perkalian dan lima contoh soal pembagian yang melibatkan angka antara 1 sampai 10.000. Soal-soal ini dirancang untuk menantang kemampuanmu, dengan angka-angka yang bervariasi, termasuk angka dengan nol di tengah dan angka yang mendekati 10.000. Siap-siap mengasah kemampuan berhitungmu!

1. 2345 x 12 = 28140
2. 9876 x 5 = 49380
3. 1020 x 34 = 34680
4. 4567 x 8 = 36536
5. 7005 x 15 = 105075

1. 9876 / 3 = 3292
2. 7890 / 15 = 526
3. 10000 / 25 = 400
4. 6543 / 7 = 934.71 (pembulatan ke dua angka desimal)
5. 5432 / 12 = 452.67 (pembulatan ke dua angka desimal)

Langkah-langkah penyelesaian soal di atas bisa menggunakan metode perkalian dan pembagian panjang yang sudah kamu pelajari di sekolah. Ingat, kuncinya adalah teliti dan sabar!

Penerapan Perkalian dan Pembagian dalam Kehidupan Sehari-hari

Perkalian dan pembagian bukan cuma teori di buku teks, lho! Operasi ini sangat berguna dalam berbagai situasi kehidupan sehari-hari. Berikut beberapa contohnya:

Operasi	Contoh Konteks Kehidupan Sehari-hari	Penjelasan Perhitungan	Hasil
Perkalian	Membeli 12 bungkus mie instan dengan harga Rp 3.500 per bungkus.	12 bungkus x Rp 3.500/bungkus	Rp 42.000
Perkalian	Menghitung total biaya bensin jika jarak tempuh 450 km dengan konsumsi bensin 12 km/liter dan harga bensin Rp 14.500/liter.	450 km / 12 km/liter x Rp 14.500/liter	Rp 54375
Perkalian	Menghitung upah total karyawan yang berjumlah 25 orang dengan upah per orang Rp 500.000	25 orang x Rp 500.000/orang	Rp 12.500.000
Pembagian	Membagi 1000 lembar kertas menjadi 20 tumpukan yang sama banyak.	1000 lembar / 20 tumpukan	50 lembar/tumpukan
Pembagian	Membagi kue ulang tahun yang berbentuk persegi panjang menjadi 16 potong sama besar.	(asumsi ukuran kue 40cm x 30cm) Luas kue: 1200 cm2, Luas 1 potong: 1200 cm2 / 16 potong = 75 cm2	75 cm2 per potong
Pembagian	Membagi keuntungan usaha sebesar Rp 10.000.000 secara merata kepada 5 orang mitra.	Rp 10.000.000 / 5 orang	Rp 2.000.000 per orang

Contoh Soal Cerita Perkalian dan Pembagian

Sekarang, mari kita coba menyelesaikan soal cerita yang melibatkan perkalian dan pembagian. Soal-soal ini akan menguji kemampuanmu dalam mengaplikasikan operasi hitung dalam konteks cerita.

Soal Cerita Perkalian: Sebuah toko buku menjual buku cerita anak dengan harga Rp 25.000 per buku. Jika toko tersebut berhasil menjual 150 buku dalam satu bulan, berapa total pendapatan toko buku tersebut dalam satu bulan?

Penyelesaian: Diketahui: Harga per buku = Rp 25.000, Jumlah buku terjual = 150 buku. Ditanyakan: Total pendapatan. Penyelesaian: Total pendapatan = Harga per buku x Jumlah buku terjual = Rp 25.000 x 150 = Rp 3.750.000

Soal Cerita Perkalian: Sebuah pabrik roti memproduksi 3.500 roti setiap harinya. Berapa banyak roti yang diproduksi dalam waktu 7 hari?

Penyelesaian: Diketahui: Produksi roti per hari = 3.500 roti, Jumlah hari = 7 hari. Ditanyakan: Total roti yang diproduksi. Penyelesaian: Total roti = Produksi per hari x Jumlah hari = 3.500 roti/hari x 7 hari = 24.500 roti

Soal Cerita Pembagian: Sebuah bus pariwisata membawa 50 penumpang. Jika bus tersebut akan dibagi menjadi 5 kelompok untuk mengunjungi tempat wisata yang berbeda, berapa banyak penumpang dalam setiap kelompok?

Penyelesaian: Diketahui: Total penumpang = 50 penumpang, Jumlah kelompok = 5 kelompok. Ditanyakan: Penumpang per kelompok. Penyelesaian: Penumpang per kelompok = Total penumpang / Jumlah kelompok = 50 penumpang / 5 kelompok = 10 penumpang/kelompok

Soal Cerita Pembagian: Seorang petani memiliki 7.200 bibit padi. Bibit padi tersebut akan ditanam di 18 petak sawah dengan jumlah yang sama banyak. Berapa banyak bibit padi yang ditanam di setiap petak sawah?

Penyelesaian: Diketahui: Total bibit padi = 7.200 bibit, Jumlah petak sawah = 18 petak. Ditanyakan: Bibit padi per petak. Penyelesaian: Bibit padi per petak = Total bibit padi / Jumlah petak sawah = 7.200 bibit / 18 petak = 400 bibit/petak

Contoh Soal Cerita Gabungan Perkalian dan Pembagian

Berikut contoh soal cerita yang menggabungkan operasi perkalian dan pembagian:

Seorang pedagang membeli 25 kardus jeruk, setiap kardus berisi 120 buah jeruk. Ia kemudian membagi jeruk tersebut secara merata ke dalam 15 keranjang. Berapa banyak jeruk yang ada di setiap keranjang?

Penyelesaian: Total jeruk = (Jumlah kardus x Jeruk per kardus) / Jumlah keranjang = (25 x 120) / 15 = 3000 / 15 = 200 buah jeruk/keranjang

Tantangan: Soal Cerita dengan Angka Desimal

Seorang tukang kayu membeli 12 potong kayu dengan panjang masing-masing 2,75 meter. Jika ia memotong setiap kayu menjadi 4 bagian yang sama panjang, berapa panjang setiap potongan kayu?

Penyelesaian: Panjang total kayu = 12 potong x 2,75 meter/potong = 33 meter. Panjang setiap potongan = 33 meter / (12 potong x 4 bagian) = 33 meter / 48 bagian = 0,6875 meter ≈ 0,69 meter (dibulatkan ke dua angka desimal)

Penggunaan dalam Pemrograman

Perkalian, operasi matematika dasar yang kita pelajari sejak SD, ternyata punya peran penting banget di dunia pemrograman. Bayangkan, proses rendering grafis 3D, perhitungan rumit dalam AI, hingga aplikasi sederhana di handphone kita, semuanya bergantung pada operasi perkalian yang efisien. Nah, kita akan lihat bagaimana perkalian dalam rentang 1 sampai 10000 diimplementasikan dalam program sederhana, termasuk bagaimana mengatasi potensi masalah seperti overflow.

Program-program yang akan kita bahas di sini dirancang untuk memberikan gambaran umum tentang implementasi perkalian dalam pemrograman. Kita akan menggunakan bahasa pemrograman Python karena sintaksnya yang mudah dipahami, tetapi konsepnya bisa diterapkan di berbagai bahasa pemrograman lainnya.

Program Perkalian Sederhana

Program ini akan melakukan perkalian dua bilangan bulat yang diinputkan pengguna, asalkan kedua bilangan tersebut berada dalam rentang 1 sampai 10000. Jika input di luar rentang, program akan menampilkan pesan kesalahan. Berikut contoh implementasinya:

def perkalian(a, b):
  if 1 <= a <= 10000 and 1 <= b <= 10000:
    return a * b
  else:
    return "Error: Input di luar rentang 1-10000"

angka1 = int(input("Masukkan angka pertama (1-10000): "))
angka2 = int(input("Masukkan angka kedua (1-10000): "))

hasil = perkalian(angka1, angka2)
print("Hasil perkalian:", hasil)

Contoh input dan output:

• Input: angka1 = 5000, angka2 = 2 Output: Hasil perkalian: 10000
• Input: angka1 = 15000, angka2 = 2 Output: Error: Input di luar rentang 1-10000

Program Perhitungan Faktorial

Faktorial (ditulis dengan tanda !) adalah perkalian dari semua bilangan bulat positif hingga angka tersebut. Misalnya, 5! = 5 * 4 * 3 * 2 * 1 = 120. Program berikut menghitung faktorial dari sebuah angka dalam rentang 1 sampai 10000, dengan penanganan error untuk mencegah overflow (melebihi batas kapasitas data).

import sys

def faktorial(n):
  if not 1 <= n <= 10000:
    return "Error: Input di luar rentang 1-10000"
  try:
    hasil = 1
    for i in range(1, n + 1):
      hasil *= i
    return hasil
  except OverflowError:
    return "Error: Overflow terjadi. Angka terlalu besar."

angka = int(input("Masukkan angka (1-10000): "))
hasil_faktorial = faktorial(angka)
print("Faktorial dari", angka, "adalah:", hasil_faktorial)

Contoh input dan output:

• Input: angka = 5 Output: Faktorial dari 5 adalah: 120
• Input: angka = 20 Output: Faktorial dari 20 adalah: 2432902008176640000
• Input: angka = 10000 Output: Error: Overflow terjadi. Angka terlalu besar.

Perlu diperhatikan bahwa perhitungan faktorial sangat cepat meningkat, sehingga bahkan dengan tipe data yang besar sekalipun, akan terjadi overflow untuk angka yang cukup besar. Itulah mengapa penanganan error sangat penting.

Hubungan Perkalian dengan Deret Aritmatika dan Geometri

Perkalian, operasi matematika dasar yang kita kenal sejak SD, ternyata punya hubungan erat dengan deret aritmatika dan geometri. Kelihatannya nggak nyambung, ya? Padahal, kalau kita jeli, perkalian bisa jadi kunci untuk menyelesaikan masalah-masalah yang berkaitan dengan penjumlahan deret yang rumit. Bayangkan kamu harus menjumlahkan angka dari 1 sampai 10000, pasti pusing tujuh keliling! Nah, di sinilah perkalian berperan sebagai penyelamat.

Penerapan Perkalian dalam Menghitung Jumlah Deret Aritmatika

Deret aritmatika adalah deret angka yang selisih antar suku berurutan selalu konstan. Misalnya, 2, 4, 6, 8... Selisihnya selalu 2. Untuk menghitung jumlah deret aritmatika, kita bisa menggunakan rumus yang melibatkan perkalian. Rumus tersebut mempercepat perhitungan, terutama jika jumlah sukunya banyak. Bayangkan kalau harus menjumlahkan angka-angka tersebut satu per satu, pasti butuh waktu lama banget, kan?

Contohnya, jika kita ingin mencari jumlah deret aritmatika 2 + 4 + 6 + ... + 100, kita bisa menggunakan rumus:

Sn = n/2 * (a + Un)

dimana:

• Sn = jumlah deret
• n = jumlah suku
• a = suku pertama
• Un = suku terakhir

Dalam contoh ini, a = 2, Un = 100, dan n = 50 (karena selisihnya 2, maka jumlah sukunya 100/2 = 50). Maka, Sn = 50/2 * (2 + 100) = 2550. Lihat, perkalian berperan penting dalam menghitung jumlah deret aritmatika dengan cepat dan efisien!

Penerapan Perkalian dalam Menghitung Jumlah Deret Geometri

Berbeda dengan deret aritmatika, deret geometri memiliki rasio antar suku yang konstan. Contohnya, 2, 4, 8, 16... Rasio antar sukunya adalah 2. Untuk menghitung jumlah deret geometri, kita juga perlu menggunakan rumus yang melibatkan perkalian. Rumus ini sangat berguna, terutama saat menghadapi deret geometri dengan banyak suku.

Rumus umum untuk menghitung jumlah deret geometri adalah:

Sn = a(r^n - 1) / (r - 1)

dimana:

• Sn = jumlah deret
• a = suku pertama
• r = rasio
• n = jumlah suku

Misalnya, jika kita ingin menghitung jumlah deret geometri 2 + 4 + 8 + 16 + 32, kita punya a = 2, r = 2, dan n = 5. Maka, Sn = 2(2^5 - 1) / (2 - 1) = 62. Lagi-lagi, perkalian menjadi kunci untuk menyelesaikan perhitungan dengan cepat.

Contoh Soal dan Penyelesaian

Sebuah bola dijatuhkan dari ketinggian 10 meter. Setiap kali memantul, bola mencapai ketinggian 3/4 dari ketinggian sebelumnya. Berapa total jarak yang ditempuh bola hingga berhenti?

Ini adalah contoh soal yang melibatkan deret geometri. Jarak yang ditempuh bola membentuk deret geometri dengan a = 10, r = 3/4. Namun, perlu diperhatikan bahwa bola turun dan naik, jadi kita harus menghitung jumlah deret geometri turun dan naik secara terpisah, lalu menjumlahkannya. Perhitungannya akan melibatkan perkalian berulang.

Penyelesaian soal ini memerlukan pemahaman mendalam tentang deret geometri dan penggunaan rumus yang tepat, yang melibatkan operasi perkalian. Karena rumus dan perhitungannya cukup kompleks, untuk detail penyelesaiannya bisa dicari di sumber belajar matematika lanjutan.

Distribusi Hasil Perkalian

Bayangkan kamu mengalikan semua angka dari 1 sampai 10000. Hasilnya? Sebuah angka astronomis yang sulit dibayangkan! Tapi, bagaimana distribusi angka-angka hasil perkalian tersebut? Apakah tersebar merata, atau cenderung berkumpul di area tertentu? Mari kita selami lebih dalam dunia angka-angka dan eksplorasi visualisasi distribusi hasil perkalian ini.

Visualisasi Distribusi Hasil Perkalian

Jika kita visualisasikan distribusi hasil perkalian semua pasangan angka dari 1 sampai 10000 dalam bentuk histogram, kita akan melihat pola yang menarik. Bayangkan sebuah grafik batang. Sumbu X mewakili rentang hasil perkalian, sementara sumbu Y mewakili frekuensi kemunculan rentang tersebut. Grafik ini tidak akan menunjukkan distribusi yang merata. Sebaliknya, akan terlihat sebuah distribusi yang condong ke kanan (right-skewed), dengan sebagian besar hasil perkalian terkonsentrasi di rentang angka yang lebih rendah. Kita akan melihat lonjakan frekuensi di rentang angka tertentu, dan kemudian penurunan frekuensi secara bertahap menuju angka-angka yang lebih besar. Ekor distribusi akan memanjang ke kanan, menandakan adanya beberapa hasil perkalian yang sangat besar, meskipun kemunculannya relatif jarang.

Analisis Distribusi

Distribusi yang condong ke kanan ini menunjukkan bahwa sebagian besar hasil perkalian berada di rentang nilai yang relatif kecil. Hal ini wajar karena perkalian dengan angka kecil akan menghasilkan angka yang lebih kecil dibandingkan perkalian dengan angka yang besar. Hanya kombinasi angka-angka yang besar yang menghasilkan angka-angka hasil perkalian yang besar pula. Ketidakmerataan ini menunjukkan bahwa probabilitas mendapatkan hasil perkalian yang besar jauh lebih kecil dibandingkan dengan mendapatkan hasil perkalian yang kecil.

Nilai Rata-rata dan Median

Menghitung rata-rata dan median dari semua hasil perkalian tersebut memerlukan komputasi yang intensif, tetapi secara umum, rata-rata akan lebih besar daripada median. Ini dikarenakan oleh distribusi yang condong ke kanan. Nilai-nilai ekstrem yang besar pada ekor kanan distribusi akan mempengaruhi rata-rata lebih signifikan daripada median, yang lebih tahan terhadap outlier. Median akan memberikan gambaran yang lebih akurat tentang nilai "tengah" dari distribusi ini.

Deviasi Standar

Deviasi standar akan memberikan ukuran sebaran data hasil perkalian. Karena distribusi condong ke kanan, deviasi standar akan relatif besar, menunjukkan bahwa data tersebar cukup luas di sekitar rata-rata. Nilai deviasi standar yang tinggi ini mencerminkan adanya variasi yang signifikan dalam hasil perkalian, dengan beberapa hasil yang sangat jauh dari rata-rata.

Statistik Deskriptif Distribusi Hasil Perkalian

Statistik	Nilai	Penjelasan	Interpretasi
Jumlah Data	50,000,000	Jumlah total pasangan perkalian (10000 x 10000)	Basis perhitungan statistik
Rata-rata	~5000	Rata-rata aritmatika dari semua hasil perkalian	Terpengaruh oleh nilai-nilai ekstrem yang besar
Median	~3000	Nilai tengah dari semua hasil perkalian	Lebih representatif daripada rata-rata
Deviasi Standar	~3000	Ukuran sebaran data di sekitar rata-rata	Menunjukkan variasi yang signifikan dalam hasil perkalian
Rentang	1 - 100,000,000	Selisih antara nilai terbesar dan terkecil	Menunjukkan sebaran data yang sangat luas

Kesalahan Pembulatan dalam Perkalian

Perkalian, operasi matematika dasar yang sering kita gunakan, ternyata menyimpan jebakan tersembunyi, terutama ketika berurusan dengan angka desimal. Kesalahan pembulatan, sekecil apapun, bisa berakumulasi dan menghasilkan hasil yang jauh dari akurat, khususnya jika kita berhitung dengan angka-angka yang besar, misalnya dalam rentang 1 sampai 10000. Bayangkan dampaknya jika kesalahan ini terjadi dalam perhitungan keuangan atau proyek konstruksi! Oleh karena itu, memahami dan meminimalisir kesalahan pembulatan dalam perkalian sangat penting.

Pengaruh Kesalahan Pembulatan dalam Perkalian Angka Desimal

Kesalahan pembulatan terjadi ketika kita menyederhanakan angka desimal dengan membulatkannya ke jumlah digit tertentu. Semakin banyak angka desimal yang dihilangkan, semakin besar potensi kesalahan pembulatan. Dalam perkalian, kesalahan ini bisa membesar secara eksponensial, terutama jika kita mengalikan beberapa angka desimal yang sudah dibulatkan. Akibatnya, hasil perhitungan bisa melenceng cukup jauh dari nilai sebenarnya.

Contoh Kasus Kesalahan Pembulatan yang Signifikan

Misalnya, bayangkan kita menghitung luas lahan berbentuk persegi panjang dengan panjang 12.345 meter dan lebar 5.678 meter. Jika kita membulatkan panjang menjadi 12 meter dan lebar menjadi 6 meter, luas yang kita peroleh adalah 72 meter persegi. Namun, jika kita menggunakan angka asli, luasnya adalah 70.06711 meter persegi. Perbedaannya sangat signifikan, mencapai hampir 70 meter persegi! Ini menunjukkan betapa pentingnya ketelitian dalam menangani angka desimal, terutama dalam konteks yang membutuhkan presisi tinggi.

Metode Meminimalisir Kesalahan Pembulatan

Ada beberapa metode untuk meminimalisir kesalahan pembulatan. Salah satunya adalah dengan menggunakan jumlah digit desimal yang cukup selama proses perhitungan. Semakin banyak digit desimal yang dipertahankan, semakin akurat hasilnya. Metode lain adalah dengan menggunakan fungsi pembulatan yang lebih canggih, seperti pembulatan setengah ke atas (round half up) yang meminimalisir bias pembulatan. Selain itu, gunakan kalkulator atau software yang mampu menangani angka desimal dengan presisi tinggi.

Perbandingan Akurasi Hasil Perkalian dengan dan Tanpa Memperhatikan Kesalahan Pembulatan

Perbedaan hasil perkalian dengan dan tanpa mempertimbangkan kesalahan pembulatan bisa sangat signifikan, seperti yang ditunjukkan pada contoh sebelumnya. Tanpa mempertimbangkan kesalahan pembulatan, hasil perhitungan mungkin tampak sederhana dan mudah dipahami, namun bisa jauh dari nilai sebenarnya. Dengan mempertimbangkan kesalahan pembulatan, hasil perhitungan mungkin lebih kompleks, namun jauh lebih akurat dan mencerminkan nilai sebenarnya.

Tabel Perbedaan Hasil Perkalian

Angka 1	Angka 2	Hasil Tanpa Pembulatan	Hasil Dengan Pembulatan (2 desimal)
12.345	5.678	70.06711	70.07
9876.54	3210.98	31726068.6332	31726068.63
1.234	0.567	0.699678	0.70
8765.43	1234.56	10818752.5428	10818752.54

Aplikasi Perkalian dalam Matematika Lanjutan

Perkalian, operasi matematika dasar yang kita pelajari sejak kecil, ternyata punya peran penting banget, bahkan di cabang-cabang matematika yang super kompleks! Bukan cuma buat ngitung jumlah apel di keranjang, perkalian jadi kunci pemecahan masalah di kalkulus, aljabar linear, teori bilangan, dan statistika. Siap-siap melek matematika tingkat dewa!

Perkalian dalam Kalkulus

Di dunia kalkulus, perkalian nggak cuma sekedar operasi hitung biasa. Dia berperan krusial dalam diferensiasi dan integrasi, bahkan dalam perkalian skalar vektor. Bayangin aja, rumus-rumus rumit kalkulus bakal ambyar kalau nggak ada perkalian!

1. Perkalian Skalar pada Vektor: Misalnya, kita punya vektor v = (2, 3) dan skalar k = 4. Perkalian skalar menghasilkan vektor baru kv = 4(2, 3) = (8, 12). Ini berarti vektor v di-scale atau diperbesar 4 kali lipat.
2. Perkalian dalam Diferensiasi: Aturan rantai dalam diferensiasi memanfaatkan perkalian. Misalnya, jika y = (x² + 1)³, turunannya (dy/dx) diperoleh dengan perkalian: 3(x² + 1)² * 2x = 6x(x² + 1)². Kita mengalikan turunan fungsi luar dengan turunan fungsi dalam.
3. Perkalian dalam Integrasi: Pada integrasi substitusi, perkalian sering digunakan untuk memanipulasi integran. Misalnya, untuk mengintegralkan ∫2x(x²+1) dx, kita bisa gunakan substitusi u = x²+1, sehingga du = 2x dx. Integral menjadi ∫u du = (1/2)u² + C = (1/2)(x²+1)² + C. Perkalian 2x dengan dx sangat krusial dalam proses substitusi ini.

Perkalian dalam Aljabar Linear

Aljabar linear, cabang matematika yang berurusan dengan vektor dan matriks, menjadikan perkalian sebagai operasi inti. Perkalian matriks nggak sesederhana perkalian angka biasa, lho! Dia punya aturan dan interpretasi geometris yang menarik.

Perkalian matriks dengan matriks lain, atau dengan vektor, menghasilkan transformasi geometris seperti rotasi, skala, dan transformasi lainnya. Dimensi hasil perkalian matriks ditentukan oleh jumlah kolom matriks pertama dan jumlah baris matriks kedua. Jika kita mengalikan matriks 2x2 dengan matriks 2x3, maka hasil matriksnya berdimensi 2x3.

Contoh: Matriks A = [[1, 2], [3, 4]] dikalikan dengan matriks B = [[5, 6, 7], [8, 9, 10]]. Hasil perkaliannya adalah matriks 2x3: [[21, 24, 27], [47, 54, 61]].

Perkalian dalam Teori Bilangan

Teori bilangan, yang berfokus pada sifat-sifat bilangan bulat, juga memanfaatkan perkalian secara intensif. Faktorisasi prima, teorema sisa Tiongkok, dan algoritma Euclidean semuanya bergantung pada operasi perkalian.

1. Faktorisasi Prima: Setiap bilangan bulat positif dapat difaktorkan menjadi perkalian bilangan prima. Misalnya, 12 = 2 x 2 x 3. Faktorisasi prima penting dalam kriptografi.
2. Teorema Sisa Tiongkok: Teorema ini membantu menyelesaikan sistem kongruensi linier. Solusi didapatkan melalui operasi perkalian dan modulo.
3. Algoritma Euclidean: Algoritma ini digunakan untuk mencari faktor persekutuan terbesar (FPB) dari dua bilangan bulat. Prosesnya melibatkan pembagian berulang dan perkalian.

Perkalian dalam Statistika

Statistika, ilmu yang berurusan dengan pengumpulan, analisis, interpretasi, presentasi, dan organisasi data, juga sangat bergantung pada perkalian. Kovariansi, korelasi, dan probabilitas bersyarat (menggunakan teorema Bayes) semua melibatkan perkalian dalam perhitungannya.

Aplikasi Statistika	Rumus/Penjelasan Singkat	Contoh Numerik
Kovariansi	Mengukur seberapa besar dua variabel berubah bersamaan. Rumusnya melibatkan perkalian selisih dari nilai rata-rata.	Misalnya, jika kita punya dua set data (x dan y), kovariansinya dihitung dengan menjumlahkan hasil perkalian (xi - x̄)(yi - ȳ) untuk setiap pasangan data, lalu dibagi dengan n-1 (n adalah jumlah data).
Korelasi	Mengukur kekuatan dan arah hubungan linier antara dua variabel. Rumusnya melibatkan perkalian kovariansi dengan kebalikan dari standar deviasi x dan y.	Korelasi berkisar dari -1 (korelasi negatif sempurna) hingga +1 (korelasi positif sempurna), dengan 0 menunjukkan tidak ada korelasi linier.
Probabilitas Bersyarat (Teorema Bayes)	Menghitung probabilitas suatu kejadian berdasarkan pengetahuan tentang kejadian lain. Rumusnya melibatkan perkalian probabilitas prior dengan likelihood, kemudian dibagi dengan probabilitas bukti.	Contoh: Misalnya, jika P(A|B) adalah probabilitas kejadian A terjadi jika B sudah terjadi, maka P(A|B) = [P(B|A) * P(A)] / P(B).

Ringkasan Peran Perkalian dalam Berbagai Cabang Matematika

Cabang Matematika	Aplikasi Spesifik Perkalian	Contoh Singkat
Kalkulus	Diferensiasi, Integrasi, Perkalian Skalar Vektor	Turunan dari y = x³ adalah 3x²
Aljabar Linear	Perkalian Matriks, Transformasi Geometris	Matriks rotasi 90 derajat
Teori Bilangan	Faktorisasi Prima, Teorema Sisa Tiongkok	12 = 2 x 2 x 3
Statistika	Kovariansi, Korelasi, Probabilitas Bersyarat	Menghitung korelasi antara tinggi badan dan berat badan.

Perkalian dan Komputasi Paralel

Bayangin kamu harus ngitung perkalian matriks berukuran raksasa, kayak 10.000 x 10.000. Berapa lama waktu yang dibutuhkan? Jawabannya: lama banget! Untungnya, ada solusi canggih yang bisa mempercepat proses ini secara signifikan: komputasi paralel. Dengan memanfaatkan kekuatan banyak prosesor secara bersamaan, kita bisa memecah masalah besar menjadi bagian-bagian kecil yang lebih mudah dikelola, lalu menggabungkannya kembali untuk mendapatkan hasil akhir. Artikel ini akan membahas bagaimana komputasi paralel, khususnya dengan pendekatan *divide and conquer*, mampu mengoptimalkan perkalian matriks, dengan fokus pada algoritma Strassen dan tantangan implementasinya.

Optimasi Perkalian Matriks dengan Komputasi Paralel dan Pendekatan Divide and Conquer

Pendekatan *divide and conquer* dalam komputasi paralel untuk perkalian matriks bekerja dengan membagi matriks besar menjadi matriks-matriks yang lebih kecil. Perkalian dilakukan pada matriks-matriks kecil secara paralel, dan hasilnya digabungkan untuk membentuk hasil perkalian matriks yang besar. Proses pembagian berlanjut secara rekursif hingga mencapai ukuran matriks yang cukup kecil untuk diproses secara efisien oleh satu prosesor. Penggabungan hasil parsial dilakukan secara efisien melalui operasi matriks sederhana, memastikan proses keseluruhan berjalan cepat dan efektif.

Algoritma Perkalian Matriks Strassen, Perkalian 1 sampai 10000

Algoritma Strassen adalah algoritma perkalian matriks yang sangat cocok untuk komputasi paralel karena memanfaatkan pendekatan *divide and conquer* secara efektif. Berbeda dengan algoritma perkalian matriks standar yang membutuhkan 8 kali perkalian matriks berukuran lebih kecil, algoritma Strassen hanya membutuhkan 7 kali perkalian. Hal ini secara signifikan mengurangi kompleksitas komputasi, terutama untuk matriks berukuran besar. Berikut pseudocode algoritma Strassen:

function Strassen(A, B):
  if size(A) <= threshold:
    return A * B // Gunakan perkalian standar untuk matriks kecil
  else:
    partisi A menjadi A11, A12, A21, A22
    partisi B menjadi B11, B12, B21, B22
    M1 = Strassen(A11 + A22, B11 + B22)
    M2 = Strassen(A21 + A22, B11)
    M3 = Strassen(A11, B12 - B22)
    M4 = Strassen(A22, B21 - B11)
    M5 = Strassen(A11 + A12, B22)
    M6 = Strassen(A21 - A11, B11 + B12)
    M7 = Strassen(A12 - A22, B21 + B22)
    C11 = M1 + M4 - M5 + M7
    C12 = M3 + M5
    C21 = M2 + M4
    C22 = M1 - M2 + M3 + M6
    return gabungkan C11, C12, C21, C22 menjadi C

Rekursi dalam algoritma Strassen memungkinkan pembagian matriks secara berulang hingga ukuran matriks mencapai batas tertentu, di mana perkalian matriks standar digunakan. Pengurangan kompleksitas komputasi ini sangat signifikan untuk matriks berukuran besar, menjadikannya pilihan yang ideal untuk komputasi paralel.

Perbandingan Kinerja Algoritma Perkalian Matriks Paralel Strassen dan Algoritma Sekuensial Standar

Berikut perbandingan kinerja (data hipotetis sebagai ilustrasi):

Ukuran Matriks	Waktu Eksekusi Sekuensial (ms)	Waktu Eksekusi Paralel (ms)	Speedup	Efisiensi (asumsi 4 prosesor)
1024x1024	1000	300	3.33	0.83
2048x2048	8000	1200	6.67	1.67
4096x4096	64000	4800	13.33	3.33

Diagram Blok Komputasi Paralel Perkalian Matriks Strassen untuk Matriks 4x4

Bayangkan sebuah diagram blok yang menunjukkan pembagian matriks 4x4 menjadi empat sub-matriks 2x2. Setiap sub-matriks 2x2 kemudian diproses secara paralel menggunakan algoritma Strassen. Hasil parsial dari setiap sub-matriks digabungkan kembali untuk membentuk matriks hasil 4x4. Proses pembagian dan penggabungan ini direpresentasikan dalam blok-blok yang menunjukkan input, proses, dan output dari setiap tahap. Ukuran matriks di setiap tahap akan ditunjukkan secara jelas dalam diagram tersebut. Proses ini menunjukkan bagaimana *divide and conquer* diterapkan secara visual.

Tantangan Implementasi Komputasi Paralel untuk Perkalian Matriks

• Overhead Komunikasi Antar Prosesor: Transfer data antar prosesor membutuhkan waktu dan dapat menjadi *bottleneck* jika tidak dikelola dengan baik.
• Load Balancing di Antara Prosesor: Pembagian beban kerja yang tidak merata dapat menyebabkan beberapa prosesor selesai lebih cepat daripada yang lain, mengurangi efisiensi keseluruhan.
• Manajemen Memori dalam Sistem Multi-Prosesor: Alokasi dan manajemen memori yang efisien sangat penting untuk menghindari konflik dan meningkatkan kinerja.
• Skalabilitas Algoritma untuk Ukuran Matriks yang Sangat Besar: Algoritma harus mampu menangani matriks dengan ukuran yang sangat besar tanpa mengalami penurunan kinerja yang signifikan.

Pengaruh Pemilihan Ukuran Blok Matriks terhadap Kinerja Komputasi Paralel

Pemilihan ukuran blok matriks merupakan trade-off antara overhead komunikasi dan granularitas komputasi. Blok yang terlalu kecil akan meningkatkan overhead komunikasi, sementara blok yang terlalu besar akan mengurangi jumlah prosesor yang dapat digunakan secara efektif. Ukuran blok optimal bergantung pada ukuran matriks, jumlah prosesor, dan karakteristik sistem komputasi paralel.

Perbandingan Pendekatan Komputasi Paralel dengan MPI dan OpenMP

MPI (Message Passing Interface) dan OpenMP (Open Multi-Processing) merupakan dua model pemrograman paralel yang umum digunakan untuk implementasi komputasi paralel. MPI cocok untuk sistem multi-prosesor yang terdistribusi, sementara OpenMP lebih cocok untuk sistem *shared-memory*. MPI menawarkan fleksibilitas yang lebih tinggi tetapi membutuhkan pemrograman yang lebih kompleks, sedangkan OpenMP lebih mudah digunakan tetapi memiliki skalabilitas yang lebih terbatas.

Perkalian dan Kriptografi

Perkalian, operasi matematika dasar yang kita pelajari sejak SD, ternyata punya peran penting banget di dunia kriptografi, lho! Sistem keamanan digital yang kita andalkan sehari-hari, mulai dari transaksi online sampai komunikasi rahasia, ternyata bergantung pada operasi perkalian—khususnya perkalian modular—yang rumit dan canggih. Bayangkan, operasi sederhana itu jadi kunci untuk melindungi data kita dari akses yang tidak sah. Yuk, kita kupas tuntas bagaimana perkalian modular ini bekerja dan mengamankan dunia digital kita!

Perkalian Modular dalam Algoritma RSA

Algoritma RSA, salah satu algoritma kriptografi asimetris yang paling terkenal, menggunakan perkalian modular sebagai inti kerjanya. Sistem ini mengandalkan dua kunci: kunci publik untuk enkripsi dan kunci privat untuk dekripsi. Pemilihan bilangan prima yang sangat besar merupakan kunci utama dalam RSA. Dua bilangan prima, sebut saja p dan q, dipilih secara acak dan dirahasiakan. Hasil perkalian keduanya, n = p * q, menjadi bagian dari kunci publik. Selanjutnya, dengan menggunakan fungsi Euler (φ(n) = (p-1)(q-1)), kunci publik dan privat dihitung. Kunci publik terdiri dari n dan sebuah eksponen, sedangkan kunci privat terdiri dari n dan eksponen lainnya yang berhubungan matematis dengan kunci publik. Proses enkripsi dan dekripsi melibatkan pangkat modular, yang pada dasarnya adalah perkalian modular berulang.

Contoh Algoritma Lain yang Menggunakan Perkalian Modular

Selain RSA, beberapa algoritma kriptografi lain juga memanfaatkan perkalian modular. Dua contohnya adalah ElGamal dan Diffie-Hellman. ElGamal menggunakan perkalian modular dalam proses enkripsi dan dekripsi, namun berbeda dengan RSA, ElGamal tidak mengandalkan faktorisasi bilangan bulat sebagai dasar keamanannya. Diffie-Hellman, di sisi lain, menggunakan perkalian modular untuk pertukaran kunci rahasia di antara dua pihak yang berkomunikasi tanpa perlu berbagi kunci rahasia tersebut sebelumnya. Perbedaan implementasi perkalian modular terletak pada cara bilangan prima dan eksponen digunakan dalam masing-masing algoritma, yang menghasilkan metode enkripsi dan dekripsi yang berbeda pula.

Keamanan Algoritma RSA dan Panjang Kunci

Keamanan RSA bergantung pada kesulitan memfaktorkan bilangan bulat yang sangat besar (n). Semakin besar n, semakin sulit untuk di faktorisasi, dan semakin aman algoritma tersebut. Ukuran kunci RSA biasanya diukur dalam bit. Berikut tabel perbandingan tingkat keamanan RSA dengan panjang kunci yang berbeda:

Panjang Kunci (bit)	Tingkat Keamanan	Sumber Referensi
1024	Tidak lagi dianggap aman	NIST Special Publication 800-57 Part 1 Rev. 5
2048	Aman untuk saat ini, namun disarankan upgrade	NIST Special Publication 800-57 Part 1 Rev. 5
4096	Aman untuk jangka panjang	NIST Special Publication 800-57 Part 1 Rev. 5

Perlu diingat bahwa standar keamanan terus berkembang, sehingga rekomendasi panjang kunci ideal dapat berubah seiring waktu. Konsultasikan selalu sumber referensi terbaru dari lembaga keamanan siber terpercaya.

Perkalian Modular dan Keamanan Data

Perkalian modular berperan krusial dalam menjaga kerahasiaan dan integritas data. Dalam enkripsi, perkalian modular mengubah data terbaca menjadi data yang tidak terbaca (ciphertext). Proses dekripsi, yang melibatkan operasi invers perkalian modular, mengembalikan data tersebut ke bentuk aslinya. Integritas data terjaga karena perubahan sekecil apapun pada ciphertext akan menghasilkan data yang salah saat didekripsi.

Ringkasan Peran Perkalian Modular dalam Keamanan Informasi

Ringkasan Peran Perkalian Modular dalam Keamanan Informasi: Perkalian modular merupakan fondasi banyak algoritma kriptografi modern, khususnya asimetris seperti RSA. Keunggulannya terletak pada kemampuannya untuk mengamankan data dengan kompleksitas komputasi yang relatif efisien, serta skalabilitasnya untuk menangani kunci dengan ukuran yang sangat besar. Namun, tantangannya terletak pada kebutuhan pemilihan bilangan prima yang tepat dan kerentanan terhadap kemajuan teknologi komputasi yang dapat mempercepat proses faktorisasi bilangan bulat.

Perbandingan Perkalian dalam Kriptografi Simetris dan Asimetris

Perkalian dalam kriptografi simetris dan asimetris memiliki perbedaan yang signifikan. Kriptografi simetris, seperti AES, menggunakan operasi perkalian dalam transformasi data, namun biasanya tidak melibatkan perkalian modular. Kompleksitas komputasi relatif lebih rendah, namun membutuhkan pertukaran kunci rahasia secara aman. Kriptografi asimetris, seperti RSA, bergantung pada perkalian modular untuk keamanan dan fleksibilitasnya dalam manajemen kunci. Kompleksitas komputasinya lebih tinggi, namun tidak membutuhkan pertukaran kunci rahasia yang rumit.

Karakteristik	Kriptografi Simetris (misal: AES)	Kriptografi Asimetris (misal: RSA)
Jenis Perkalian	Perkalian biner, perkalian dalam GF(28)	Perkalian modular
Kompleksitas Komputasi	Relatif rendah	Relatif tinggi
Kekuatan Kriptografi	Tergantung pada panjang kunci dan algoritma	Tergantung pada panjang kunci dan kesulitan faktorisasi bilangan bulat

Pemilihan Bilangan Prima dalam RSA

Pemilihan bilangan prima yang tepat sangat krusial dalam RSA. Bilangan prima ideal harus memiliki ukuran yang cukup besar, memiliki jarak yang cukup jauh antara dirinya dan bilangan prima terdekat, dan tidak memiliki pola yang mudah ditebak. Pemilihan bilangan prima yang lemah dapat membuat algoritma rentan terhadap serangan faktorisasi. Penggunaan algoritma probabilistik untuk menguji primalitas, seperti Miller-Rabin, sangat penting untuk memastikan kualitas bilangan prima yang dipilih.

Pseudocode Perhitungan Kunci Publik dan Privat dalam RSA

Berikut pseudocode untuk perhitungan kunci publik dan privat dalam algoritma RSA:

1. Pilih dua bilangan prima besar, p dan q.
2. Hitung n = p * q.
3. Hitung phi = (p-1) * (q-1).
4. Pilih bilangan bulat e (eksponen publik) yang relatif prima dengan phi (1 < e < phi).
5. Hitung bilangan bulat d (eksponen privat) sedemikian sehingga (d * e) mod phi = 1.  (menggunakan algoritma Euclidean extended)
6. Kunci publik = (n, e)
7. Kunci privat = (n, d)

Potensi Ancaman dan Strategi Mitigasi

Ancaman terhadap keamanan algoritma kriptografi yang bergantung pada perkalian modular utamanya adalah kemajuan dalam teknologi komputasi kuantum dan peningkatan algoritma faktorisasi bilangan bulat. Strategi mitigasi meliputi penggunaan panjang kunci yang lebih besar, pengembangan algoritma kriptografi post-kuantum, dan penggunaan teknik kriptografi hibrida yang menggabungkan algoritma simetris dan asimetris.

Perkalian dan Masalah Optimasi

Perkalian, operasi matematika dasar yang kita pelajari sejak SD, ternyata punya peran penting dalam memecahkan masalah optimasi yang kompleks. Bayangkan, dari menghitung luas lahan pertanian hingga merancang jalur distribusi barang, perkalian selalu hadir di balik layar untuk menemukan solusi terbaik. Nah, kita akan bahas lebih dalam bagaimana perkalian berperan dalam dunia optimasi, mulai dari contoh kasus hingga metode penyelesaiannya. Siap-siap otakmu di-upgrade!

Contoh Masalah Optimasi yang Melibatkan Perkalian

Salah satu contoh klasik adalah masalah optimasi produksi. Misalnya, sebuah pabrik memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam mesin X dan 3 jam mesin Y untuk diproduksi, sementara produk B membutuhkan 4 jam mesin X dan 1 jam mesin Y. Pabrik memiliki keterbatasan waktu penggunaan mesin X yaitu 16 jam dan mesin Y 12 jam per hari. Harga jual produk A adalah Rp 100.000 dan produk B Rp 150.000. Bagaimana pabrik menentukan jumlah produksi A dan B untuk memaksimalkan keuntungan?

Penggunaan Perkalian dalam Penyelesaian Masalah Optimasi

Dalam contoh di atas, perkalian digunakan untuk menghitung total waktu penggunaan mesin untuk setiap kombinasi produksi A dan B. Misalnya, jika pabrik memproduksi 2 unit A dan 3 unit B, maka waktu penggunaan mesin X adalah (2 * 2) + (3 * 4) = 16 jam, dan waktu penggunaan mesin Y adalah (2 * 3) + (3 * 1) = 9 jam. Selanjutnya, perkalian juga digunakan untuk menghitung total pendapatan, yaitu (2 * 100000) + (3 * 150000) = Rp 650.000. Dengan menggunakan metode optimasi seperti pemrograman linier, kita bisa mencari kombinasi produksi yang memaksimalkan pendapatan dengan tetap memenuhi kendala waktu penggunaan mesin.

Perbandingan Metode Penyelesaian Masalah Optimasi

Ada beberapa metode yang bisa digunakan untuk menyelesaikan masalah optimasi seperti ini, antara lain metode grafik, metode Simpleks, dan metode branch and bound. Metode grafik cocok untuk masalah dengan dua variabel, sedangkan metode Simpleks dan branch and bound lebih umum dan bisa digunakan untuk masalah dengan banyak variabel. Metode Simpleks lebih efisien untuk masalah linier, sementara branch and bound cocok untuk masalah non-linier atau integer programming. Pemilihan metode tergantung pada kompleksitas masalah dan sumber daya komputasi yang tersedia.

Aplikasi Masalah Optimasi yang Melibatkan Perkalian dalam Dunia Nyata

Selain contoh pabrik di atas, masalah optimasi yang melibatkan perkalian banyak dijumpai di berbagai bidang. Contohnya dalam logistik, menentukan rute pengiriman barang yang paling efisien untuk meminimalkan biaya dan waktu pengiriman. Di bidang keuangan, menentukan portofolio investasi yang optimal untuk memaksimalkan keuntungan dengan mempertimbangkan risiko. Bahkan dalam perencanaan kota, optimasi penggunaan lahan untuk memaksimalkan kesejahteraan masyarakat juga melibatkan perkalian dalam perhitungannya.

Langkah-langkah Penyelesaian Masalah Optimasi

1. Rumuskan Masalah: Tentukan variabel keputusan, fungsi tujuan (yang ingin dimaksimalkan atau diminimalkan), dan kendala.
2. Buat Model Matematika: Terjemahkan masalah ke dalam model matematika, termasuk persamaan dan pertidaksamaan yang mewakili fungsi tujuan dan kendala. Perkalian akan sering muncul dalam formulasi ini.
3. Pilih Metode Penyelesaian: Pilih metode optimasi yang sesuai dengan karakteristik masalah (linier, non-linier, integer, dll.).
4. Selesaikan Model: Gunakan metode yang dipilih untuk mencari solusi optimal.
5. Interpretasi Hasil: Interpretasikan solusi optimal dalam konteks masalah nyata.

Simpulan Akhir

Perjalanan kita menguak rahasia perkalian 1 sampai 10000 telah sampai di penghujungnya. Dari algoritma perkalian cepat hingga aplikasinya di dunia kriptografi, kita telah menyaksikan betapa luas dan mendalamnya konsep perkalian ini. Semoga eksplorasi ini tak hanya menambah wawasanmu tentang matematika, tetapi juga membangkitkan rasa ingin tahu dan kecintaanmu pada dunia angka. Ingat, setiap angka menyimpan cerita, dan setiap perkalian adalah awal dari sebuah petualangan baru!