5,29 Dibulatkan Menjadi Berapa?

5 29 dibulatkan menjadi – 5,29 dibulatkan menjadi berapa? Pertanyaan sederhana yang mungkin sering muncul dalam kehidupan sehari-hari, mulai dari menghitung uang belanja hingga menganalisis data ilmiah. Membulatkan angka desimal memang terlihat mudah, tapi ternyata ada aturan dan metode yang perlu dipahami agar hasilnya akurat dan sesuai konteks. Pernah bingung membulatkan angka yang berakhir dengan angka 5? Yuk, kita kupas tuntas!

Pembulatan angka desimal, khususnya angka 5,29, bergantung pada tingkat ketelitian yang diinginkan. Apakah kita ingin membulatkan ke satuan terdekat, puluhan terdekat, atau bahkan mempertahankan beberapa angka di belakang koma? Metode pembulatan yang berbeda akan menghasilkan hasil yang berbeda pula. Artikel ini akan membahas berbagai metode pembulatan, aturannya, dan penerapannya dalam berbagai konteks, termasuk keuangan dan ilmu pengetahuan. Siap-siap kuasai seni membulatkan angka!

Pembulatan Bilangan Desimal

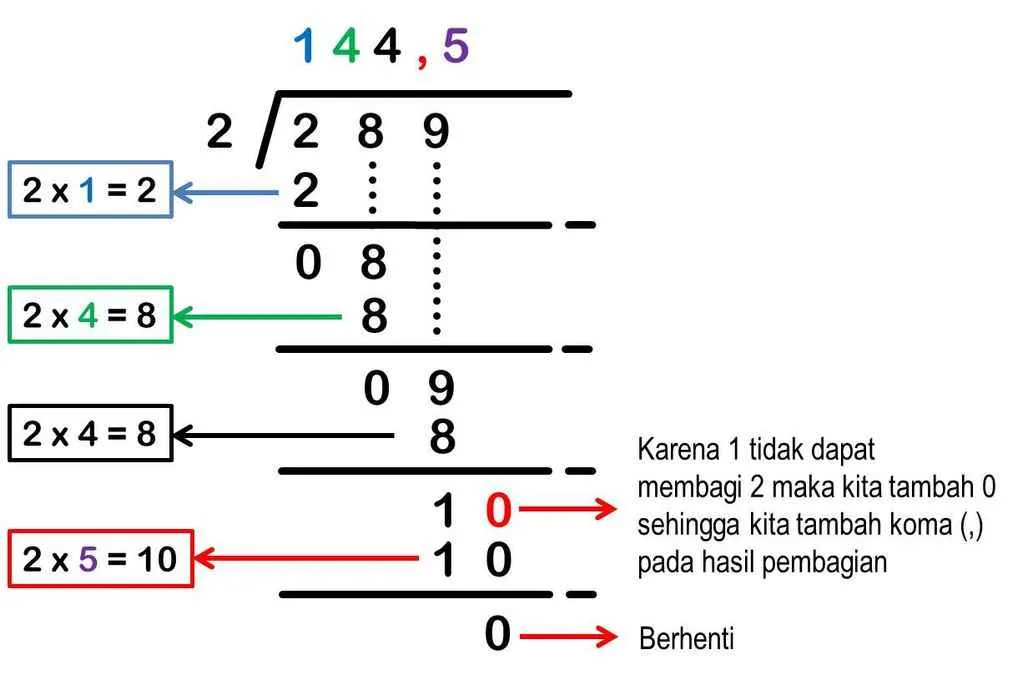
Pernah bingung saat harus membulatkan angka desimal? Tenang, membulatkan angka itu sebenarnya gampang kok! Kita sering banget ketemu angka desimal dalam kehidupan sehari-hari, mulai dari harga barang di supermarket sampai nilai ujian. Nah, biar nggak bingung lagi, yuk kita bahas cara membulatkan bilangan desimal dengan contoh-contoh yang mudah dipahami.

Cara Membulatkan Bilangan Desimal ke Atas dan ke Bawah

Membulatkan bilangan desimal bisa dilakukan ke atas atau ke bawah, tergantung angka di belakang koma. Secara umum, jika angka di belakang koma lebih besar atau sama dengan 5, maka dibulatkan ke atas. Sebaliknya, jika kurang dari 5, dibulatkan ke bawah. Berikut tabelnya:

Angka Desimal	Pembulatan ke Atas	Pembulatan ke Bawah
5,29	5,3	5,2
7,82	7,8	7,8
3,55	3,6	3,5
9,49	9,5	9,4

Pembulatan 5,29 ke Satuan Terdekat

Untuk membulatkan 5,29 ke satuan terdekat, kita lihat angka di belakang koma. Angka di belakang koma adalah 29. Karena 29 kurang dari 50, maka 5,29 dibulatkan ke bawah menjadi 5.

Contoh Pembulatan Bilangan Desimal Lainnya

Berikut beberapa contoh pembulatan bilangan desimal lainnya:

• 8,76 dibulatkan ke satuan terdekat: Angka di belakang koma adalah 76. Karena 76 lebih besar dari 50, maka 8,76 dibulatkan ke atas menjadi 9.
• 2,3 dibulatkan ke satuan terdekat: Angka di belakang koma adalah 3. Karena 3 kurang dari 5, maka 2,3 dibulatkan ke bawah menjadi 2.
• 12,5 dibulatkan ke satuan terdekat: Angka di belakang koma adalah 5. Karena 5 sama dengan 5, maka 12,5 dibulatkan ke atas menjadi 13.

Langkah-Langkah Pembulatan Bilangan Desimal

Secara umum, langkah-langkah pembulatan bilangan desimal adalah sebagai berikut:

1. Tentukan tempat desimal yang ingin dibulatkan (satuan, puluhan, ratusan, dst).
2. Lihat angka di sebelah kanan tempat desimal yang ingin dibulatkan.
3. Jika angka tersebut 5 atau lebih besar dari 5, bulatkan angka di tempat desimal yang ingin dibulatkan ke atas (tambah 1).
4. Jika angka tersebut kurang dari 5, biarkan angka di tempat desimal yang ingin dibulatkan tetap.
5. Buang angka di belakang tempat desimal yang ingin dibulatkan.

Pembulatan 5,29 ke Puluhan Terdekat

Untuk membulatkan 5,29 ke puluhan terdekat, kita perlu melihat angka puluhannya. Angka puluhannya adalah 0 (karena 5,29 bisa ditulis sebagai 05,29). Karena angka satuannya (5) lebih besar atau sama dengan 5, maka kita bulatkan ke atas. Jadi, 5,29 dibulatkan ke puluhan terdekat menjadi 10.

Aturan Pembulatan

Pernah bingung pas ngitung nilai ujian dan angka di belakang koma bikin pusing? Tenang, pembulatan angka desimal itu gampang kok! Artikel ini bakal ngebahas tuntas soal aturan pembulatan, khususnya untuk angka 5,29. Kita akan bahas algoritmanya, flowchart-nya, dan bedanya pembulatan ke atas sama ke bawah. Siap-siap kuasai ilmu pembulatan!

Algoritma Pembulatan Bilangan Desimal

Algoritma pembulatan itu sebenarnya simpel. Intinya, kita lihat angka di belakang koma. Kalau angka di belakang koma itu 5 atau lebih, kita bulatkan ke atas. Kalau kurang dari 5, kita bulatkan ke bawah. Gampang kan? Misalnya, 5,29. Angka di belakang koma adalah 29. Karena 2 kurang dari 5, maka 5,29 dibulatkan menjadi 5.

Aturan Pembulatan untuk Bilangan 5,29

Nah, sekarang kita terapkan algoritma tadi ke angka 5,29. Angka di belakang koma adalah 29. Karena 2 (angka pertama di belakang koma) kurang dari 5, maka sesuai aturan pembulatan, 5,29 dibulatkan ke bawah menjadi 5.

Flowchart Pembulatan

Buat visualisasi proses pembulatan, kita bisa pakai flowchart. Bayangkan flowchart-nya seperti ini: Mulai -> Ambil angka desimal -> Lihat angka di belakang koma -> Kurang dari 5? -> Ya (bulatkan ke bawah) -> Tidak (bulatkan ke atas) -> Hasil -> Selesai. Simpel dan mudah dipahami, kan?

Perbedaan Pembulatan ke Atas dan ke Bawah

Pembulatan ke atas dan ke bawah itu beda tipis, tapi dampaknya bisa signifikan, lho! Pembulatan ke atas artinya kita naikin angka ke satuan terdekat yang lebih besar. Contohnya, 5,6 dibulatkan ke atas jadi 6. Sedangkan pembulatan ke bawah, kita turunin angka ke satuan terdekat yang lebih kecil. Contohnya, 5,2 dibulatkan ke bawah jadi 5.

• Pembulatan ke Atas: Angka di belakang koma ≥ 5, dibulatkan ke atas. Contoh: 7,5 menjadi 8, 3,8 menjadi 4.
• Pembulatan ke Bawah: Angka di belakang koma < 5, dibulatkan ke bawah. Contoh: 7,4 menjadi 7, 3,2 menjadi 3.

Kasus Khusus dalam Pembulatan Bilangan Desimal

Ada beberapa kasus khusus yang perlu diperhatikan. Misalnya, angka yang tepat di tengah-tengah, seperti 5,5. Ada beberapa metode untuk kasus ini, bisa dibulatkan ke atas, ke bawah, atau dibulatkan ke angka genap terdekat. Metode yang digunakan biasanya tergantung konteks perhitungannya.

Angka	Pembulatan ke Atas	Pembulatan ke Bawah	Pembulatan ke Genap Terdekat
5,5	6	5	6
4,5	5	4	4

Penerapan Pembulatan dalam Konteks

Pembulatan, sekilas terlihat sepele, nyatanya punya peran krusial dalam berbagai aspek kehidupan. Dari urusan keuangan hingga perhitungan ilmiah yang presisi, pembulatan berdampak signifikan terhadap hasil akhir. Yuk, kita telusuri lebih dalam bagaimana pembulatan bekerja dan pengaruhnya!

Penerapan Pembulatan dalam Konteks Keuangan

Dalam dunia keuangan, akurasi adalah segalanya. Namun, pembulatan seringkali diperlukan untuk menyederhanakan angka dan mempermudah transaksi. Berikut beberapa contohnya:

Contoh	Nilai Awal	Metode Pembulatan	Nilai Setelah Pembulatan	Dampak terhadap Total
Harga Jual Barang	Rp 12.375	Pembulatan ke atas	Rp 12.400	Peningkatan pendapatan sedikit
Pajak Penghasilan	Rp 2.783.500	Pembulatan ke bawah	Rp 2.783.000	Pengurangan pajak yang dibayarkan
Saldo Rekening	Rp 9.876.123,50	Pembulatan ke angka terdekat	Rp 9.876.124	Perubahan minimal, tidak signifikan

Pentingnya Pembulatan dalam Pengukuran Ilmiah

Dalam pengukuran ilmiah, tingkat akurasi sangat penting. Pembulatan berperan dalam menjaga konsistensi dan menghindari penyajian data yang menyesatkan. Signifikansi angka menjadi kunci dalam menentukan tingkat pembulatan yang tepat.

Tingkat akurasi yang dicapai bergantung pada metode pembulatan dan jumlah angka signifikan yang dipertahankan. Pembulatan ke angka terdekat umumnya memberikan keseimbangan antara akurasi dan kesederhanaan, sementara pembulatan ke atas atau ke bawah digunakan ketika konservatisme diperlukan. Penggunaan metode pembulatan yang tepat sangat penting untuk menghindari kesalahan interpretasi data. Misalnya, dalam pengukuran massa suatu zat kimia, pembulatan yang salah dapat mempengaruhi perhitungan konsentrasi dan reaksi kimia.

Tari Bedhaya Ketawang Berasal Dari Mana?

Pengaruh Pembulatan terhadap Hasil Perhitungan

Pembulatan dapat memengaruhi hasil perhitungan aritmatika. Kesalahan pembulatan, meskipun kecil, dapat terakumulasi dan menyebabkan penyimpangan yang signifikan, terutama dalam perhitungan kompleks.

Contoh 1 (Penjumlahan): 12,34 + 5,67 = 18,01. Jika dibulatkan ke satuan terdekat menjadi 12 + 6 = 18. Selisihnya kecil.

Contoh 2 (Perkalian): 12,34 x 5,67 = 70,0278. Jika dibulatkan menjadi 12 x 6 = 72. Selisihnya lebih signifikan.

Skenario Pembulatan yang Berpengaruh Signifikan

Ada situasi di mana pembulatan berdampak besar pada hasil akhir. Berikut dua skenario:

• Pembulatan Bunga Pinjaman: Pembulatan bunga pinjaman ke atas, meskipun terlihat kecil per bulannya, akan berakumulasi menjadi jumlah yang signifikan dalam jangka panjang. Hal ini akan berdampak pada total cicilan yang harus dibayarkan.
• Pembulatan Jumlah Suara dalam Pemilihan: Dalam pemilihan yang ketat, pembulatan jumlah suara dapat mengubah hasil pemilihan. Jika perbedaan suara sangat tipis, pembulatan dapat menentukan pemenang.

Dampak Pembulatan pada Perhitungan Statistik

Pembulatan dapat mempengaruhi perhitungan statistik deskriptif seperti rata-rata, median, dan standar deviasi. Penggunaan metode pembulatan yang tepat sangat penting untuk memastikan akurasi hasil analisis.

Sebagai contoh, pembulatan data mentah sebelum menghitung rata-rata dapat menghasilkan nilai rata-rata yang sedikit berbeda dibandingkan jika perhitungan dilakukan dengan data mentah yang tidak dibulatkan. Metode pembulatan yang direkomendasikan dalam konteks statistik adalah pembulatan ke angka terdekat, kecuali ada alasan khusus untuk menggunakan metode lain.

Analisis Kesalahan Pembulatan

Kesalahan pembulatan dapat diukur menggunakan kesalahan absolut dan relatif. Kesalahan absolut adalah selisih antara nilai sebenarnya dan nilai yang dibulatkan. Kesalahan relatif dihitung dengan membagi kesalahan absolut dengan nilai sebenarnya, kemudian dikalikan 100% untuk mendapatkan persentase.

Contoh: Nilai sebenarnya = 12,345. Nilai dibulatkan = 12. Kesalahan absolut = 0,345. Kesalahan relatif = (0,345/12,345) x 100% ≈ 2,79%.

Metode Pembulatan yang Berbeda

Terdapat beberapa metode pembulatan, masing-masing dengan kelebihan dan kekurangannya. Pemilihan metode yang tepat bergantung pada konteks dan tingkat akurasi yang dibutuhkan.

• Pembulatan ke Atas: Selalu membulatkan ke angka yang lebih besar.
• Pembulatan ke Bawah: Selalu membulatkan ke angka yang lebih kecil.
• Pembulatan ke Angka Terdekat: Membulatkan ke angka terdekat; jika angka di belakang koma 5 atau lebih, dibulatkan ke atas; jika kurang dari 5, dibulatkan ke bawah.
• Pembulatan Setengah ke Atas: Jika angka di belakang koma 5, dibulatkan ke atas; jika kurang dari 5, dibulatkan ke bawah.

Perbandingan Metode Pembulatan

Ngomongin angka, pasti nggak lepas dari proses pembulatan. Bayangin aja, kalau kita lagi ngitung biaya proyek, atau menghitung rata-rata nilai ujian. Pembulatan jadi hal penting banget biar angkanya lebih gampang dipahami dan diinterpretasi. Tapi, tau nggak sih, ternyata ada beberapa metode pembulatan yang bisa kita gunakan? Nah, di artikel ini, kita akan bahas perbandingan beberapa metode pembulatan, mulai dari yang paling umum sampai yang mungkin belum pernah kamu dengar!

Metode Pembulatan Standar (Pembulatan ke Atas atau ke Bawah)

Metode pembulatan standar adalah metode yang paling umum digunakan. Cara kerjanya sederhana banget: lihat angka di belakang koma. Kalau angka tersebut 5 atau lebih, maka dibulatkan ke atas. Kalau kurang dari 5, dibulatkan ke bawah. Contohnya, 3,7 dibulatkan menjadi 4, sedangkan 3,2 dibulatkan menjadi 3.

Kelebihan metode ini adalah simpel dan mudah dipahami. Hampir semua orang sudah familiar dengan metode ini. Kekurangannya? Metode ini bisa menyebabkan bias, terutama jika kita melakukan pembulatan berkali-kali. Akumulasi pembulatan bisa menghasilkan error yang cukup signifikan.

Metode Pembulatan ke Atas

Sesuai namanya, metode ini selalu membulatkan angka ke atas, tanpa peduli berapa angka di belakang koma. Misalnya, 3,1 dibulatkan menjadi 4, dan 3,9 juga dibulatkan menjadi 4.

Kelebihannya? Metode ini cocok digunakan ketika kita ingin memastikan hasil akhir selalu lebih besar dari nilai aslinya, misalnya untuk perhitungan stok barang agar tidak kekurangan. Kekurangannya jelas, yaitu hasil pembulatan akan selalu lebih besar dari nilai sebenarnya, sehingga bisa menyebabkan overestimasi.

Metode Pembulatan ke Bawah

Kebalikan dari metode pembulatan ke atas, metode ini selalu membulatkan angka ke bawah, berapapun angka di belakang koma. Contohnya, 3,1 dan 3,9 keduanya dibulatkan menjadi 3.

Kelebihan metode ini adalah hasil pembulatan akan selalu lebih kecil dari nilai sebenarnya, cocok untuk situasi di mana kita ingin menghindari overestimasi. Kekurangannya, metode ini bisa menyebabkan underestimasi yang signifikan.

Tabel Perbandingan Metode Pembulatan

Metode Pembulatan	Deskripsi	Kelebihan	Kekurangan
Standar	Membulatkan ke atas jika angka di belakang koma ≥ 5, ke bawah jika < 5	Simpel dan mudah dipahami	Bisa menyebabkan bias jika dilakukan berulang kali
Ke Atas	Selalu membulatkan ke atas	Menjamin hasil selalu lebih besar dari nilai asli	Memungkinkan overestimasi
Ke Bawah	Selalu membulatkan ke bawah	Menjamin hasil selalu lebih kecil dari nilai asli	Memungkinkan underestimasi

Ilustrasi Perbedaan Hasil Pembulatan

Bayangkan kita punya tiga angka: 3,4; 3,5; dan 3,6. Dengan metode standar, 3,4 dibulatkan menjadi 3, 3,5 menjadi 4, dan 3,6 menjadi 4. Dengan metode pembulatan ke atas, ketiganya menjadi 4. Sedangkan dengan metode pembulatan ke bawah, ketiganya menjadi 3. Perbedaan ini menunjukkan bagaimana pemilihan metode pembulatan bisa sangat berpengaruh pada hasil akhir.

Pemilihan Metode Pembulatan yang Tepat

Pemilihan metode pembulatan yang tepat bergantung pada konteks permasalahannya. Jika akurasi sangat penting dan pembulatan berulangkali, mungkin metode standar dengan mempertimbangkan akumulasi error adalah pilihan terbaik. Namun, jika kita perlu memastikan hasil selalu lebih besar atau lebih kecil dari nilai sebenarnya, maka metode pembulatan ke atas atau ke bawah bisa jadi pilihan yang lebih tepat. Misalnya, dalam perhitungan biaya proyek, lebih baik menggunakan pembulatan ke atas untuk menghindari kekurangan dana.

Contoh Kasus Perbedaan Hasil Pembulatan

Sebuah toko online menjual barang dengan harga Rp 12.750 per unit. Jika ada 1000 unit yang terjual, total pendapatan sebenarnya adalah Rp 12.750.000. Jika menggunakan metode pembulatan standar, harga per unit dibulatkan menjadi Rp 13.000, sehingga total pendapatan menjadi Rp 13.000.000. Perbedaannya Rp 250.000! Ini menunjukkan betapa pentingnya memilih metode pembulatan yang tepat, terutama dalam konteks bisnis.

Penggunaan Pembulatan dalam Pemrogragan: 5 29 Dibulatkan Menjadi

Pembulatan angka desimal merupakan operasi umum dalam pemrograman, terutama saat berurusan dengan data numerik yang memerlukan representasi yang lebih sederhana atau saat kita ingin menampilkan hasil perhitungan dengan tingkat presisi tertentu. Proses pembulatan ini melibatkan beberapa metode, seperti pembulatan ke atas, ke bawah, dan pembulatan ke nilai terdekat. Pemahaman yang baik tentang berbagai teknik pembulatan dan implementasinya dalam bahasa pemrograman seperti Python dan JavaScript sangat penting untuk memastikan akurasi dan efisiensi dalam aplikasi.

Pseudocode untuk Fungsi Pembulatan

Berikut adalah pseudocode untuk fungsi pembulatan bilangan desimal ke atas, ke bawah, dan pembulatan terdekat. Perbedaan utama terletak pada bagaimana fungsi tersebut menangani bagian pecahan dari angka.

• Pembulatan ke Atas (ceil): Jika bagian pecahan lebih besar dari 0, bulatkan ke bilangan bulat terdekat yang lebih besar. Jika bagian pecahan adalah 0, kembalikan angka tersebut.
• Pembulatan ke Bawah (floor): Buang bagian pecahan dan kembalikan bilangan bulat yang lebih kecil.
• Pembulatan Terdekat (round): Jika bagian pecahan lebih besar atau sama dengan 0.5, bulatkan ke atas. Jika kurang dari 0.5, bulatkan ke bawah.

Fungsi Pembulatan dalam Python dan JavaScript

Baik Python maupun JavaScript menyediakan fungsi bawaan untuk ketiga jenis pembulatan tersebut. Perbedaan utama terletak pada nama fungsi dan bagaimana mereka menangani angka negatif. Secara umum, semua fungsi ini akan membulatkan angka negatif ke arah bilangan bulat yang lebih kecil (kecuali `ceil` yang membulatkan ke arah yang lebih besar).

• Python: math.ceil(), math.floor(), round()
• JavaScript: Math.ceil(), Math.floor(), Math.round()

Contoh Implementasi Kode Pembulatan

Berikut contoh implementasi dalam Python dan JavaScript, termasuk contoh dengan angka negatif dan nol:

Python:


import math

print(math.ceil(2.3)) # Output: 3
print(math.floor(2.3)) # Output: 2
print(round(2.3)) # Output: 2
print(math.ceil(-2.3)) # Output: -2
print(math.floor(-2.3))# Output: -3
print(round(-2.3)) # Output: -2
print(round(0)) # Output: 0

JavaScript:


console.log(Math.ceil(2.3)); // Output: 3
console.log(Math.floor(2.3)); // Output: 2
console.log(Math.round(2.3)); // Output: 2
console.log(Math.ceil(-2.3)); // Output: -2
console.log(Math.floor(-2.3));// Output: -3
console.log(Math.round(-2.3));// Output: -2
console.log(Math.round(0)); // Output: 0


Fungsi Pembulatan dalam Library Math

Library	Fungsi	Deskripsi	Parameter Input	Jenis Pembulatan
Python (math)	math.ceil()	Pembulatan ke atas	Bilangan desimal	Ke Atas
Python (math)	math.floor()	Pembulatan ke bawah	Bilangan desimal	Ke Bawah
Python (math)	round()	Pembulatan ke bilangan bulat terdekat	Bilangan desimal	Terdekat
JavaScript	Math.ceil()	Pembulatan ke atas	Bilangan desimal	Ke Atas
JavaScript	Math.floor()	Pembulatan ke bawah	Bilangan desimal	Ke Bawah
JavaScript	Math.round()	Pembulatan ke bilangan bulat terdekat	Bilangan desimal	Terdekat

Penanganan Error dalam Fungsi Pembulatan

Jika input bukan angka, fungsi pembulatan di Python dan JavaScript akan menghasilkan error. Untuk menangani hal ini, kita bisa menggunakan blok try-except. Berikut contohnya dalam Python:


import math

def round_safe(x):
try:
return round(x)
except TypeError:
return "Input harus berupa angka"

print(round_safe(3.14)) # Output: 3
print(round_safe("abc")) # Output: Input harus berupa angka


Perbandingan Performa Fungsi Pembulatan

Library numerik tingkat lanjut seperti NumPy di Python menawarkan fungsi pembulatan yang dioptimalkan untuk array besar. NumPy umumnya lebih cepat daripada fungsi pembulatan bawaan untuk operasi pada array besar karena vektorisasi. Perbedaan waktu eksekusi akan semakin terlihat seiring bertambahnya ukuran array.

Fungsi Pembulatan Khusus

Berikut contoh fungsi pembulatan khusus dalam Python yang menerima angka desimal dan jumlah digit desimal yang diinginkan sebagai input:


def round_to_decimal(number, decimal_places):
factor = 10 decimal_places
return round(number * factor) / factor

print(round_to_decimal(3.14159, 2)) # Output: 3.14


Pembulatan dan Presisi

Pernah ngebayangin gimana rasanya kalo saldo rekening kita tiba-tiba berubah drastis gara-gara pembulatan? Atau hasil perhitungan ilmiah meleset jauh karena angka dibulatkan sembarangan? Pembulatan, sekilas terlihat sepele, ternyata punya peran krusial dalam akurasi data dan hasil perhitungan. Makanya, penting banget buat kita ngerti hubungan antara pembulatan dan presisi, biar nggak salah langkah dalam berbagai konteks, mulai dari urusan keuangan sampai riset ilmiah.

Hubungan Pembulatan dan Presisi Angka

Presisi angka mengacu pada seberapa dekat suatu nilai pengukuran atau perhitungan dengan nilai sebenarnya. Pembulatan, di sisi lain, adalah proses penyederhanaan angka dengan mengurangi jumlah digit signifikan. Semakin banyak digit yang dihilangkan saat pembulatan, semakin rendah presisi angka yang dihasilkan. Bayangin aja, kalo kita membulatkan angka 3,14159 ke 3,14, kita kehilangan beberapa digit yang sebenarnya berkontribusi pada presisi nilai tersebut. Semakin banyak digit yang kita buang, semakin besar potensi kesalahan akibat pembulatan.

Ilustrasi Pengaruh Pembulatan terhadap Presisi

Misalnya, kita punya dua pengukuran panjang: 12,345 cm dan 12,346 cm. Kalo kita bulatkan keduanya ke satu desimal, hasilnya sama-sama 12,3 cm. Meskipun awalnya kedua nilai tersebut berbeda, setelah pembulatan, perbedaannya hilang. Ini menunjukkan bagaimana pembulatan bisa mengurangi presisi dan bahkan menghilangkan perbedaan penting antara dua nilai.

Ilustrasi lain: Coba bayangkan kita menghitung luas lahan dengan panjang 12,345 meter dan lebar 8,765 meter. Hasil perhitungan tepatnya adalah 108,172075 meter persegi. Jika kita membulatkan panjang dan lebar ke satu desimal (12,3 meter dan 8,8 meter), luas yang dihitung menjadi 108,14 meter persegi. Perbedaannya memang kecil, tetapi dalam konteks perhitungan luas lahan yang besar, kesalahan akumulasi bisa jadi signifikan.

Contoh Kasus Pentingnya Presisi dan Pembulatan Hati-hati

Dalam dunia medis, presisi sangat penting. Misalnya, dalam pemberian dosis obat, pembulatan yang ceroboh bisa berakibat fatal. Sebuah dosis obat yang seharusnya 2,5 mg, jika dibulatkan menjadi 3 mg, bisa menyebabkan overdosis. Begitu juga dalam rekayasa, pembulatan yang salah dalam perhitungan struktur bangunan bisa berujung pada bencana.

Signifikansi Angka dan Kaitannya dengan Pembulatan

Signifikansi angka menunjukkan tingkat ketelitian suatu pengukuran. Angka signifikan merupakan digit-digit yang dipercaya akurat dalam suatu pengukuran. Saat melakukan pembulatan, kita harus memperhatikan angka signifikan untuk meminimalisir kesalahan. Pembulatan yang tepat harus mempertimbangkan angka signifikan yang ada untuk mempertahankan akurasi hasil.

Strategi Meminimalkan Kesalahan Akibat Pembulatan

Ada beberapa strategi untuk meminimalisir kesalahan akibat pembulatan. Pertama, gunakan jumlah digit signifikan yang cukup selama perhitungan. Kedua, lakukan pembulatan hanya pada tahap akhir perhitungan. Ketiga, gunakan metode pembulatan yang tepat, misalnya pembulatan ke atas atau ke bawah, tergantung konteksnya. Terakhir, selalu periksa kembali hasil perhitungan untuk memastikan akurasi.

Pembulatan dan Ketidakpastian

Pernah ngalamin situasi di mana hasil pengukuran sedikit melenceng dari ekspektasi? Itulah ketidakpastian pengukuran, sesuatu yang umum terjadi dalam berbagai bidang, dari sains hingga teknik. Pembulatan angka, yang sering kita lakukan secara otomatis, ternyata punya peran krusial dalam menangani ketidakpastian ini. Artikel ini akan membahas bagaimana ketidakpastian muncul, bagaimana pembulatan berperan, dan bagaimana kita bisa menyajikan hasil pengukuran secara akurat dan bertanggung jawab.

Sumber-Sumber Ketidakpastian dalam Pengukuran

Ketidakpastian dalam pengukuran bisa berasal dari berbagai sumber. Ketelitian alat ukur, kesalahan manusia, dan bahkan kesalahan sistematis dalam proses pengukuran semuanya berkontribusi. Bayangkan kamu lagi ngukur panjang meja pakai penggaris. Penggarisnya mungkin kurang presisi, kamu mungkin salah baca skala, atau bahkan ada sedikit perbedaan karena posisi penggaris yang nggak pas. Semua itu sumber ketidakpastian!

• Kesalahan Alat Ukur: Penggaris yang aus atau rusak, timbangan yang belum dikalibrasi, semua bisa menyebabkan ketidakakuratan.
• Kesalahan Manusia: Kesalahan dalam membaca skala, kesalahan dalam mencatat data, atau bahkan kesalahan dalam melakukan pengukuran itu sendiri.
• Kesalahan Sistematis: Kesalahan yang konsisten terjadi karena faktor tertentu, misalnya suhu ruangan yang mempengaruhi panjang suatu benda.

Misalnya, kita ukur panjang sebuah benda lima kali dan mendapatkan data: 10.1 cm, 10.2 cm, 10.3 cm, 10.2 cm, 10.1 cm. Ketidakpastian absolutnya adalah setengah dari rentang data, yaitu 0.1 cm. Ketidakpastian relatifnya adalah ketidakpastian absolut dibagi rata-rata data, sekitar 1%.

Pengukuran (cm)	Ketidakpastian Absolut (cm)	Ketidakpastian Relatif (%)
10.1	0.1	0.99
10.2	0.1	0.98
10.3	0.1	0.97
10.2	0.1	0.98
10.1	0.1	0.99

Angka Penting dan Ketidakpastian Pengukuran

Angka penting mencerminkan tingkat ketelitian pengukuran. Semakin banyak angka penting, semakin teliti pengukuran tersebut. Saat melakukan perhitungan dengan data yang memiliki ketidakpastian, kita perlu mempertimbangkan angka penting untuk menghindari penyajian hasil yang terlalu presisi.

Contoh: 12.345 + 6.78 = 19.125. Karena 6.78 hanya memiliki tiga angka penting, hasil akhirnya harus dibulatkan menjadi 19.1. Perkalian dan pembagian juga mengikuti aturan angka penting. Perhitungan yang mempertimbangkan angka penting memberikan gambaran yang lebih realistis tentang ketidakpastian hasil.

Pengaruh Pembulatan terhadap Interpretasi Hasil

Pembulatan yang tidak tepat dapat menyesatkan interpretasi hasil. Misalnya, membulatkan hasil pengukuran konsentrasi obat dari 2.54 mg/ml menjadi 3 mg/ml bisa menyebabkan dosis yang diberikan terlalu tinggi atau rendah, dengan konsekuensi yang signifikan. Grafik batang yang membandingkan hasil pengukuran sebenarnya dengan hasil yang dibulatkan akan menunjukkan perbedaan yang mungkin tampak kecil, namun berdampak besar.

Bayangkan grafik batang dengan sumbu X menunjukkan pengukuran sebenarnya dan sumbu Y menunjukkan selisih antara hasil yang dibulatkan dan sebenarnya. Kita akan melihat beberapa titik data menunjukkan selisih yang cukup signifikan, terutama jika angka yang dibulatkan adalah 5.

Panduan Pembulatan dengan Ketidakpastian

Panduan Pembulatan:

1. Tentukan ketidakpastian pengukuran.
2. Tentukan angka penting yang sesuai dengan ketidakpastian.
3. Bulatkan hasil pengukuran sesuai dengan angka penting yang ditentukan. Jika angka terakhir yang akan dibulatkan adalah 5, bulatkan ke angka genap terdekat.
4. Tuliskan hasil akhir dengan ketidakpastiannya (misalnya, 10.2 ± 0.1 cm).

Contoh Kasus Ketidakpastian yang Signifikan

Berikut dua contoh kasus di mana ketidakpastian berpengaruh signifikan:

Sains: Pengukuran konsentrasi suatu zat dalam eksperimen kimia. Ketidakpastian dalam pengukuran dapat mempengaruhi kesimpulan penelitian. Tabel data mentah, perhitungan ketidakpastian, dan hasil pembulatan yang tepat akan menunjukkan bagaimana ketidakpastian diatasi.

Teknik: Perhitungan beban maksimum yang dapat ditahan oleh sebuah jembatan. Ketidakpastian dalam perhitungan dapat menyebabkan kegagalan struktur. Tabel yang serupa untuk kasus teknik ini akan menunjukkan pentingnya mempertimbangkan ketidakpastian dalam perancangan.

Konsep Signifikan Figure

Bayangin kamu lagi ngukur panjang meja pakai penggaris. Penggarisnya cuma akurat sampai milimeter, jadi nggak mungkin kamu bisa ngasih hasil pengukuran sampai tingkat mikrometer, kan? Nah, konsep angka signifikan ini mirip kayak gitu. Dia ngatur seberapa akurat hasil pengukuran atau perhitungan kita, dan seberapa banyak angka yang “berarti” dalam suatu nilai. Angka signifikan penting banget, terutama dalam sains dan teknik, karena menentukan tingkat kepercayaan kita terhadap hasil pengukuran atau perhitungan.

Angka signifikan adalah angka yang menunjukkan tingkat ketelitian suatu pengukuran atau perhitungan. Angka yang tidak signifikan adalah angka yang hanya sebagai penanda posisi desimal dan tidak memberikan informasi tambahan tentang ketelitian. Perbedaannya terletak pada seberapa pasti angka tersebut mewakili nilai sebenarnya. Contohnya, 0.0025 hanya memiliki dua angka signifikan (2 dan 5), karena nol di depan koma hanya sebagai penanda posisi desimal. Sementara 2500 bisa memiliki dua, tiga, atau empat angka signifikan, tergantung konteksnya (apakah nol di belakang angka 5 pasti atau hanya sebagai penanda posisi ribuan). Notasi ilmiah, seperti 2.50 x 10³, jelas menunjukkan tiga angka signifikan karena nol di belakang angka 5 menunjukkan ketelitian sampai dua tempat desimal.

Menentukan Jumlah Angka Signifikan

Menentukan jumlah angka signifikan penting untuk memahami tingkat ketelitian data. Berikut ini beberapa contoh dan penjelasannya:

Angka	Jumlah Angka Signifikan	Penjelasan
0.0025	2	Nol di depan koma bukan angka signifikan.
2500	2 (atau 3, atau 4, tergantung konteks)	Nol di belakang angka 5 bisa signifikan atau tidak, tergantung konteksnya. Jika diketahui presisi sampai ratusan, maka ada 3 angka signifikan (250). Jika presisi sampai ribuan, maka ada 4 angka signifikan (2500). Jika presisi hanya sampai puluhan, maka ada 2 angka signifikan (2500 dibulatkan menjadi 2500).
2.50 x 103	3	Nol di belakang angka 5 menunjukkan ketelitian sampai dua tempat desimal.
100.0	4	Nol di belakang koma menunjukkan ketelitian sampai satu tempat desimal.
0.01020	4	Nol di depan koma bukan angka signifikan, sedangkan nol di antara angka 1 dan 2 serta nol di belakang angka 2 merupakan angka signifikan.

Aturan Pembulatan Berdasarkan Angka Signifikan

Pembulatan angka berdasarkan angka signifikan memastikan konsistensi dan akurasi hasil. Aturannya sederhana: lihat angka di belakang angka signifikan terakhir. Jika angka tersebut 5 atau lebih, bulatkan ke atas. Jika kurang dari 5, bulatkan ke bawah.

Contoh: Bulatkan 3.14159 ke tiga angka signifikan. Angka signifikan terakhir adalah 4. Angka selanjutnya adalah 1 (kurang dari 5), jadi dibulatkan menjadi 3.14. Sedangkan 3.14659 dibulatkan menjadi 3.15 karena angka setelah 4 adalah 6 (lebih besar dari 5).

Pentingnya Angka Signifikan dalam Pengolahan Data Ilmiah

Menggunakan angka signifikan dengan benar sangat krusial dalam sains. Ketelitian data sangat bergantung padanya. Berikut beberapa alasannya:

• Akurasi Hasil: Angka signifikan menunjukkan tingkat ketelitian pengukuran dan perhitungan, sehingga hasil yang dilaporkan lebih akurat dan mencerminkan ketidakpastian yang ada.
• Mencegah Kesalahan Interpretasi Data: Menggunakan angka signifikan yang tepat menghindari interpretasi data yang salah dan kesimpulan yang keliru. Misalnya, jika kita melaporkan konsentrasi suatu zat dengan angka signifikan yang terlalu banyak, kita mungkin memberikan kesan bahwa ketelitian pengukuran lebih tinggi daripada yang sebenarnya.
• Konsistensi dalam Pelaporan: Penggunaan angka signifikan yang konsisten dalam pelaporan ilmiah memastikan bahwa data mudah dipahami dan dibandingkan oleh peneliti lain.

Contoh kasus: Bayangkan penelitian tentang efek suatu obat. Jika dosis obat dilaporkan dengan angka signifikan yang tidak tepat, bisa saja menyebabkan kesimpulan yang salah tentang efektivitas dan keamanan obat tersebut.

Metode Menjaga Angka Signifikan dalam Perhitungan

Untuk menjaga angka signifikan selama perhitungan, kita perlu memperhatikan aturan khusus untuk setiap operasi aritmatika.

Penjumlahan dan Pengurangan: Hasil perhitungan dibatasi oleh angka dengan jumlah desimal paling sedikit.
Perkalian dan Pembagian: Jumlah angka signifikan hasil perhitungan dibatasi oleh angka dengan jumlah angka signifikan paling sedikit.

Contoh: 2.50 x 10³ + 1.2 x 10² = 2.62 x 10³. Karena 1.2 x 10² hanya memiliki dua angka signifikan, maka hasilnya dibulatkan ke dua angka signifikan.

Contoh Soal dan Jawaban

Berikut beberapa contoh soal dan jawaban yang berkaitan dengan konsep angka signifikan:

1. Soal Mudah: Berapa jumlah angka signifikan dalam angka 12.00?
2. Soal Sedang: Bulatkan 0.004567 ke dua angka signifikan.
3. Soal Sulit: Hitung (1.23 x 10⁴) x (4.5 x 10^-2) dan nyatakan hasilnya dengan jumlah angka signifikan yang tepat.

Jawaban:

1. Empat angka signifikan.
2. 0.0046
3. (1.23 x 10⁴) x (4.5 x 10^-2) = 5.535 x 10². Karena 4.5 x 10^-2 hanya memiliki dua angka signifikan, maka hasilnya dibulatkan menjadi 5.5 x 10².

Pembulatan dalam Matematika

Hayo ngaku, siapa di sini yang pernah bingung pas lagi ngitung uang kembalian terus angka desimalnya ribet banget? Atau pas lagi hitung-hitung nilai ujian, angka-angkanya bikin pusing? Tenang, ada solusi mudahnya kok! Kita bakal bahas tentang pembulatan dalam matematika, suatu konsep sederhana tapi super penting yang sering kita pakai dalam kehidupan sehari-hari.

Konsep Pembulatan

Pembulatan adalah cara untuk menyederhanakan angka dengan mengubahnya menjadi angka yang lebih mudah diingat dan dihitung. Ada dua jenis pembulatan dasar: pembulatan ke atas dan pembulatan ke bawah. Bayangin gini, kalau angka di belakang koma lebih dari atau sama dengan 5, kita bulatkan ke atas. Kalau kurang dari 5, kita bulatkan ke bawah. Gampang kan?

Contoh Penerapan Pembulatan dalam Operasi Matematika

Pembulatan nggak cuma buat angka desimal aja lho! Kita juga bisa pakai buat angka bulat. Nih, beberapa contoh penerapan pembulatan dalam berbagai operasi matematika:

1. Penjumlahan: 2,7 + 3,2 ≈ 6 (dibulatkan ke satuan terdekat)
2. Pengurangan: 15,8 – 7,3 ≈ 9 (dibulatkan ke satuan terdekat)
3. Perkalian: 4,6 x 2,1 ≈ 10 (dibulatkan ke satuan terdekat)
4. Pembagian: 25,5 / 5 ≈ 5 (dibulatkan ke satuan terdekat)
5. Gabungan Operasi: (12,3 + 8,8) / 3 ≈ 7 (dibulatkan ke satuan terdekat. Langkah: 12,3 + 8,8 = 21,1; 21,1 / 3 ≈ 7)

Tabel Pembulatan Berbagai Bilangan

Berikut tabel yang menunjukkan hasil pembulatan berbagai bilangan dengan berbagai tingkat presisi. Kita bisa lihat betapa angka-angka itu berubah setelah dibulatkan.

Bilangan Asli	Pembulatan ke Satuan	Pembulatan ke Puluhan	Pembulatan ke Ratusan	Pembulatan ke Ribuan
2345,67	2346	2350	2300	2000
-123,45	-123	-120	-100	0
7890,12	7890	7890	7900	8000
-5678,90	-5679	-5680	-5700	-6000
12345,5	12346	12350	12300	12000
-9876,4	-9876	-9880	-9900	-10000
345,6	346	350	300	0
-876,5	-877	-880	-900	-1000
1000,1	1000	1000	1000	1000
-12,3	-12	-10	0	0

Perbedaan Pembulatan dan Pemotongan

Pembulatan dan pemotongan (truncation) berbeda. Pembulatan mempertimbangkan angka di belakang koma untuk menentukan arah pembulatan, sedangkan pemotongan hanya membuang angka di belakang koma. Contoh: 3,7 dibulatkan menjadi 4, tetapi dipotong menjadi 3. Pemotongan lebih tepat digunakan ketika kita perlu menghilangkan bagian desimal tanpa mempengaruhi nilai keseluruhan, misalnya dalam konteks penghitungan jumlah barang.

Jenis-jenis Pembulatan

Ada beberapa jenis pembulatan, selain pembulatan ke atas dan ke bawah yang sudah kita bahas. Pemilihan jenis pembulatan bergantung pada konteksnya.

• Pembulatan ke angka signifikan: Membulatkan angka ke jumlah digit tertentu yang dianggap penting. Misalnya, 12345 dibulatkan ke tiga angka signifikan menjadi 12300.
• Pembulatan setengah ke atas: Jika angka di belakang koma adalah 5, maka dibulatkan ke atas. Misalnya, 2,5 menjadi 3.
• Pembulatan banker’s rounding: Mirip dengan setengah ke atas, tetapi jika angka di belakang koma adalah 5 dan angka sebelumnya genap, maka dibulatkan ke bawah. Jika ganjil, dibulatkan ke atas. Ini untuk mengurangi bias pembulatan.

Pengaruh Pembulatan terhadap Akurasi

Pembulatan dapat mempengaruhi akurasi hasil perhitungan, terutama jika dilakukan berulang kali. Misalnya, dalam perhitungan keuangan, pembulatan yang tidak tepat dapat menyebabkan kesalahan yang signifikan, terutama jika jumlahnya besar.

Algoritma Pembulatan Bilangan Desimal

Berikut pseudocode untuk algoritma pembulatan bilangan desimal:

FUNCTION roundDecimal(number, decimalPlaces)
  factor = 10 ^ decimalPlaces
  roundedNumber = ROUND(number * factor) / factor
  RETURN roundedNumber
END FUNCTION

Soal Latihan Pembulatan

Yuk, kita coba beberapa soal latihan!

1. Bulatkan 34,56 ke satuan terdekat. (Jawaban: 35)
2. Bulatkan 1234,5 ke puluhan terdekat. (Jawaban: 1230)
3. Bulatkan -2345,67 ke ratusan terdekat. (Jawaban: -2300)
4. Bulatkan 9876,5 ke ribuan terdekat. (Jawaban: 10000)
5. Bulatkan 0,0045 ke perseribuan terdekat. (Jawaban: 0,005)

Pembulatan dalam Kehidupan Sehari-hari

Pembulatan sering kita jumpai dalam kehidupan sehari-hari, seperti pembulatan harga barang di toko, perhitungan uang kembalian, dan perhitungan nilai rata-rata.

Pembulatan dan Statistika

Pernah ngerasa ribet ngitung data statistik, apalagi kalau angkanya desimal melulu? Nah, pembulatan hadir sebagai solusi praktis. Tapi, jangan sampai asal bulatin aja, ya! Soalnya, pembulatan bisa berpengaruh besar ke hasil analisis data. Artikel ini bakal ngebahas peran penting pembulatan dalam statistika deskriptif, dampaknya ke perhitungan, dan strategi biar nggak salah kaprah.

Peran Pembulatan dalam Statistika Deskriptif

Pembulatan dalam statistika deskriptif berfungsi untuk menyederhanakan data mentah yang seringkali berupa angka desimal panjang. Proses ini mempermudah interpretasi data, membuat presentasi data lebih ringkas, dan mempercepat perhitungan. Namun, perlu diingat bahwa pembulatan juga bisa menimbulkan sedikit kesalahan atau bias, sehingga perlu kehati-hatian dalam penerapannya.

Pengaruh Pembulatan pada Perhitungan Rata-rata, Median, dan Modus

Pembulatan angka bisa mengubah nilai rata-rata, median, dan modus, walaupun terkadang perubahannya kecil. Misalnya, rata-rata nilai ujian siswa sebelum pembulatan adalah 7,85. Setelah dibulatkan ke angka satuan, rata-ratanya menjadi 8. Perbedaannya mungkin terlihat kecil, tapi dalam data skala besar, akumulasi kesalahan pembulatan bisa signifikan. Begitu pula dengan median dan modus, nilai keduanya bisa sedikit berubah setelah pembulatan, tergantung pada sebaran data dan aturan pembulatan yang digunakan.

Perbandingan Hasil Statistika Sebelum dan Sesudah Pembulatan

Statistika	Sebelum Pembulatan	Sesudah Pembulatan
Rata-rata Nilai Ujian	78.65	79
Median Tinggi Badan (cm)	165.3	165
Modus Ukuran Sepatu	40.5	41

Tabel di atas menunjukkan contoh perbedaan hasil statistika sebelum dan sesudah pembulatan. Perbedaannya memang kecil, tetapi perlu dipertimbangkan, terutama jika analisis data membutuhkan presisi tinggi.

Implikasi Pembulatan pada Analisis Data Statistik

Pembulatan yang tidak tepat dapat menyebabkan bias dalam analisis data statistik. Hal ini bisa mengakibatkan kesimpulan yang salah atau interpretasi data yang keliru. Oleh karena itu, penting untuk mempertimbangkan tingkat presisi yang dibutuhkan dan memilih metode pembulatan yang sesuai dengan konteks analisis data. Misalnya, dalam riset medis, pembulatan yang kurang tepat bisa berdampak fatal.

Strategi Meminimalisir Bias Akibat Pembulatan dalam Analisis Statistik

Untuk meminimalisir bias akibat pembulatan, beberapa strategi bisa diterapkan. Pertama, gunakan angka desimal yang cukup hingga tahap perhitungan akhir. Kedua, gunakan metode pembulatan yang konsisten, misalnya pembulatan ke atas atau ke bawah, atau pembulatan ke angka terdekat. Ketiga, laporkan hasil perhitungan sebelum dan sesudah pembulatan untuk membandingkan dan mengevaluasi tingkat kesalahan. Terakhir, perhatikan konteks analisis data dan tentukan tingkat presisi yang dibutuhkan sebelum melakukan pembulatan.

Kasus Khusus Pembulatan

Pembulatan angka, kelihatannya simpel ya? Angka di atas 5 dibulatkan ke atas, di bawah 5 dibulatkan ke bawah. Gampang! Tapi, tunggu dulu. Ada beberapa kasus khusus yang bisa bikin kamu garuk-garuk kepala, terutama saat berurusan dengan angka yang berakhir dengan 5 atau angka nol di belakang koma. Yuk, kita bahas detailnya!

Pembulatan Bilangan Berakhiran Lima

Nah, ini dia yang sering bikin bingung. Kalau angka di belakang koma adalah 5, apakah dibulatkan ke atas atau ke bawah? Jawabannya: tergantung! Beberapa metode pembulatan menggunakan aturan “pembulatan ke angka genap”. Artinya, jika angka di depan 5 adalah genap, maka dibulatkan ke bawah. Sebaliknya, jika angka di depan 5 adalah ganjil, maka dibulatkan ke atas. Metode lain mungkin hanya membulatkan ke atas secara konsisten. Konsistensi dalam metode pembulatan sangat penting untuk menghindari bias dan kesalahan interpretasi data.

Pembulatan Bilangan dengan Nol di Belakang Koma

Angka dengan nol di belakang koma sebenarnya tidak perlu dibulatkan. Misalnya, 2,000 tetap 2. Namun, konteksnya penting. Jika angka tersebut merupakan hasil perhitungan dan memiliki angka di belakang koma, meski nol, maka perlu dipertimbangkan tingkat presisi yang dibutuhkan. Mungkin kita perlu membulatkan ke angka desimal tertentu, tergantung keperluan dan tingkat ketelitian yang diinginkan. Misalnya, 2,0001 bisa dibulatkan menjadi 2,00 atau 2, tergantung tingkat ketelitian yang diinginkan.

Contoh Kasus Pembulatan yang Berbeda Metode

Bayangkan kita punya angka 2,5. Metode pembulatan ke angka genap akan menghasilkan 2, karena angka di depan 5 (yaitu 2) adalah genap. Namun, metode pembulatan ke atas akan menghasilkan 3. Begitu pula dengan angka 3,5. Metode pembulatan ke angka genap akan menghasilkan 4, sementara metode pembulatkan ke atas akan menghasilkan 4 juga. Perbedaan ini bisa berdampak signifikan, terutama dalam perhitungan yang melibatkan banyak data.

Pedoman Penanganan Kasus Khusus Pembulatan

• Tentukan metode pembulatan yang akan digunakan dan konsisten dengan metode tersebut.
• Pertimbangkan tingkat presisi yang dibutuhkan sebelum melakukan pembulatan.
• Jika memungkinkan, gunakan metode pembulatan ke angka genap untuk meminimalisir bias.
• Selalu dokumentasikan metode pembulatan yang digunakan untuk transparansi dan reproduksibilitas hasil.

Potensi Kesalahan pada Kasus Khusus Pembulatan

Kesalahan paling umum adalah ketidakkonsistenan dalam metode pembulatan. Menggunakan metode yang berbeda untuk data yang berbeda dapat menghasilkan hasil yang bias dan menyesatkan. Selain itu, kurangnya pemahaman tentang tingkat presisi yang dibutuhkan juga bisa menyebabkan kesalahan interpretasi data. Misalnya, membulatkan angka penjualan hingga ke satuan rupiah, ketika sebenarnya angka tersebut mewakili jutaan rupiah, akan menghasilkan kesalahan yang signifikan.

Perbandingan dengan Fungsi Pembulatan di Spreadsheet

Ngomongin pembulatan angka, pasti udah familiar banget, kan? Baik itu manual pas lagi itung-itung belanjaan di warung, atau pakai fitur canggih di spreadsheet kayak Excel atau Google Sheets. Nah, di artikel ini kita bakal bedah tuntas perbedaan metode pembulatan manual sama fungsi-fungsi keren di spreadsheet. Siap-siap melek angka!

Metode Pembulatan: Perbandingan Manual vs. Spreadsheet

Pembulatan manual biasanya kita lakukan dengan cara sederhana: ke atas, ke bawah, atau ke angka terdekat. Sementara di spreadsheet, ada fungsi-fungsi khusus yang lebih akurat dan efisien. Berikut perbandingannya:

Angka	Pembulatan ke Atas (Manual)	Pembulatan ke Bawah (Manual)	Pembulatan Terdekat (Manual)	ROUND (Excel/Sheets)	ROUNDUP (Excel/Sheets)	ROUNDDOWN (Excel/Sheets)
12.52	13	12	13	13	13	12
12.47	13	12	12	12	13	12
12.555	13	12	13	13	13	12

Contoh di atas menunjukkan bagaimana hasil pembulatan bisa berbeda, tergantung metode yang digunakan. Fungsi ROUND di spreadsheet mirip dengan pembulatan terdekat secara manual, sedangkan ROUNDUP selalu membulatkan ke atas, dan ROUNDDOWN selalu membulatkan ke bawah.

Fungsi Pembulatan di Berbagai Program Spreadsheet

Microsoft Excel, Google Sheets, dan LibreOffice Calc punya fungsi pembulatan yang beragam. Ketiganya punya fungsi dasar yang serupa, tapi ada juga yang spesifik.

Program	Fungsi	Deskripsi	Sintaks
Excel/Sheets/Calc	ROUND	Membulatkan ke angka desimal tertentu.	ROUND(number, num_digits)
Excel/Sheets/Calc	ROUNDUP	Membulatkan ke atas ke angka desimal tertentu.	ROUNDUP(number, num_digits)
Excel/Sheets/Calc	ROUNDDOWN	Membulatkan ke bawah ke angka desimal tertentu.	ROUNDDOWN(number, num_digits)
Excel	MROUND	Membulatkan ke kelipatan tertentu.	MROUND(number, multiple)

Perbedaan utama terletak pada arah pembulatan. ROUND membulatkan ke angka terdekat, ROUNDUP selalu ke atas, dan ROUNDDOWN selalu ke bawah. Fungsi MROUND unik karena memungkinkan pembulatan ke kelipatan angka tertentu, misalnya kelipatan 1000.

Contoh Perhitungan dengan Fungsi Pembulatan, 5 29 dibulatkan menjadi

Berikut beberapa contoh penerapan fungsi pembulatan dalam perhitungan:

1. Total Harga Barang (Pembulatan ke Atas ke Ribuan Terdekat): Misal total harga barang Rp 1.234.567. Rumus di spreadsheet: =ROUNDUP(1234567,-3). Hasilnya: Rp 1.235.000.
2. Rata-rata Nilai Ujian (Pembulatan ke Satu Desimal): Misal nilai ujian: 85, 90, 78, 82, 95. Rumus di spreadsheet: =ROUND(AVERAGE(85,90,78,82,95),1). Hasilnya: 86.0
3. Diskon Harga (Pembulatan ke Bawah ke Ratusan Terdekat): Misal harga awal Rp 57.890, diskon 10%. Rumus di spreadsheet: =ROUNDDOWN(57890*0.1,-2). Hasilnya: Rp 5.700.

Bayangkan spreadsheet yang menampilkan perhitungan ini dengan jelas, lengkap dengan rumus dan hasilnya. Ini memudahkan kita dalam memeriksa dan memahami proses perhitungan.

Kelebihan dan Kekurangan Fungsi Pembulatan di Spreadsheet

Fungsi pembulatan di spreadsheet punya sisi positif dan negatif yang perlu kita perhatikan.

• Kelebihan: Otomatisasi proses, konsistensi hasil, efisiensi waktu.
• Kekurangan: Potensi kesalahan pembulatan signifikan jika tidak hati-hati, keterbatasan fungsi pembulatan tertentu.

Ketepatan dan efisiensi adalah kunci. Pilihlah fungsi yang tepat sesuai kebutuhan, dan selalu periksa kembali hasilnya untuk memastikan keakuratan.

Tutorial Singkat Penggunaan Fungsi Pembulatan di Google Sheets

Berikut langkah-langkah singkat menggunakan fungsi ROUND, ROUNDUP, dan ROUNDDOWN di Google Sheets:

1. Buka Google Sheets dan buat lembar kerja baru.
2. Masukkan data angka yang ingin dibulatkan di sel-sel tertentu.
3. Di sel lain, masukkan rumus: =ROUND(A1,2) (untuk membulatkan angka di sel A1 ke 2 desimal), =ROUNDUP(A1,2) (membulatkan ke atas), atau =ROUNDDOWN(A1,2) (membulatkan ke bawah).
4. Tekan Enter. Hasil pembulatan akan muncul di sel tersebut.

Contoh: Jika sel A1 berisi 12.345, maka =ROUND(A1,2) akan menghasilkan 12.35, =ROUNDUP(A1,2) menghasilkan 12.35, dan =ROUNDDOWN(A1,2) menghasilkan 12.34.

Penanganan Kasus Khusus Pembulatan

Angka nol dan angka negatif perlu penanganan khusus dalam pembulatan. Angka nol akan tetap nol setelah dibulatkan, apapun metodenya. Untuk angka negatif, pembulatan ke atas akan menghasilkan angka negatif yang lebih besar (lebih dekat ke nol), sedangkan pembulatan ke bawah akan menghasilkan angka negatif yang lebih kecil (lebih jauh dari nol).

Contoh: ROUND(-12.5,0) menghasilkan -13 (pembulatan terdekat), ROUNDUP(-12.5,0) menghasilkan -12, dan ROUNDDOWN(-12.5,0) menghasilkan -13.

Akurasi dan Pembulatan

Pembulatan, sekilas terlihat sepele, nyatanya punya peran krusial dalam akurasi perhitungan. Bayangkan, kesalahan sekecil apapun bisa berdampak besar, terutama di bidang yang membutuhkan presisi tinggi seperti keuangan, sains, dan teknik. Artikel ini akan mengupas tuntas bagaimana pembulatan mempengaruhi hasil perhitungan dan strategi untuk meminimalisir kesalahannya.

Pengaruh Pembulatan terhadap Akurasi Perhitungan

Pembulatan mempengaruhi akurasi hasil perhitungan aritmatika dasar. Pada penjumlahan dan pengurangan, kesalahan pembulatan bersifat akumulatif. Semakin banyak angka yang dijumlahkan atau dikurangkan, semakin besar potensi kesalahan. Perkalian dan pembagian juga rentan terhadap kesalahan pembulatan, terutama jika angka yang terlibat memiliki banyak digit desimal. Kesalahan ini bisa diperbesar jika operasi aritmatika dikombinasikan.

Contoh Kasus Kesalahan Pembulatan yang Signifikan

Berikut tiga contoh bagaimana kesalahan pembulatan bisa berdampak besar:

1. Keuangan: Bunga Majemuk. Misalnya, investasi Rp10.000.000 dengan bunga 10% per tahun. Jika bunga dibulatkan ke angka terdekat setiap tahun, setelah 10 tahun, selisihnya bisa mencapai ratusan ribu rupiah dibandingkan perhitungan tanpa pembulatan.
2. Ilmu Pengetahuan: Perhitungan Fisika. Dalam perhitungan lintasan peluru, pembulatan kecil pada kecepatan awal atau sudut elevasi bisa menghasilkan perbedaan yang signifikan pada titik jatuh peluru, khususnya pada jarak tembak yang jauh.
3. Teknik: Perhitungan Konstruksi. Pembulatan dimensi bangunan, misalnya panjang atau lebar, meski hanya beberapa milimeter, bisa mengakibatkan kesalahan yang signifikan pada keseluruhan struktur, terutama dalam bangunan tinggi atau jembatan.

Hubungan Tingkat Pembulatan dan Akurasi Hasil Perhitungan √2 * π * 10

Tabel berikut menunjukkan hubungan antara tingkat pembulatan dan akurasi hasil perhitungan √2 * π * 10 (dengan π = 3.14159265359):

Tingkat Pembulatan (Desimal)	Hasil Pembulatan	Nilai Sebenarnya (≈ 44.42882938158)	Selisih	Persentase Kesalahan Relatif
0	44	44.42882938158	0.42882938158	0.965%
1	44.4	44.42882938158	0.02882938158	0.065%
2	44.43	44.42882938158	0.00117061842	0.003%
3	44.429	44.42882938158	0.00017061842	0.0004%

Pentingnya Akurasi dalam Perhitungan yang Melibatkan Pembulatan

Menjaga akurasi dalam perhitungan sangat penting, terutama dalam sistem embedded dengan resource terbatas dan sistem kritis seperti sistem kontrol penerbangan atau sistem medis. Kesalahan pembulatan yang kecil bisa berakibat fatal dalam sistem-sistem tersebut.

Strategi Meminimalisir Kesalahan Pembulatan

Beberapa strategi dapat diterapkan untuk meminimalisir kesalahan pembulatan:

• Penjumlahan Kompensasi: Metode ini mengurangi kesalahan akumulatif dalam penjumlahan sejumlah besar angka dengan menyimpan dan menambahkan sisa-sisa pembulatan. Contoh: jumlahkan angka-angka kecil terlebih dahulu, kemudian jumlahkan dengan angka-angka besar.
• Aritmatika Presisi Ganda: Menggunakan tipe data dengan presisi lebih tinggi (misalnya, double dibandingkan float) dapat meningkatkan akurasi, tetapi membutuhkan lebih banyak memori dan waktu komputasi.
• Pembulatan Terarah: Pembulatan ke atas selalu membulatkan ke angka yang lebih besar, pembulatan ke bawah selalu ke angka yang lebih kecil, dan pembulatan ke angka terdekat membulatkan ke angka terdekat. Pemilihan metode bergantung pada konteks dan toleransi kesalahan yang diperbolehkan.

Implementasi Strategi Meminimalisir Kesalahan Pembulatan (Pseudocode)

Berikut pseudocode untuk menghitung rata-rata sekumpulan angka dengan penjumlahan kompensasi:

function rataRata(angka[]):
  jumlah = 0
  sisa = 0
  for each x in angka:
    temp = jumlah + x + sisa
    jumlah = floor(temp) // Pembulatan ke bawah
    sisa = temp - jumlah
  return jumlah / length(angka)

Perbandingan Metode Pembulatan

Metode Pembulatan	Contoh	Hasil	Dampak terhadap Akurasi
Ke Atas	2.3	3	Meningkatkan nilai, potensi overestimation
Ke Bawah	2.7	2	Menurunkan nilai, potensi underestimation
Ke Angka Terdekat	2.4	2	Menghasilkan nilai yang paling mendekati, tetapi masih mungkin terjadi kesalahan

Pengaruh Tipe Data terhadap Akurasi

Tipe data seperti float, double, dan decimal memiliki presisi yang berbeda. Float memiliki presisi lebih rendah daripada double, sementara decimal menawarkan presisi desimal yang lebih tinggi. Pemilihan tipe data yang tepat sangat penting untuk memastikan akurasi perhitungan.

// Contoh dalam Java
float floatValue = 2.345f;
double doubleValue = 2.345;
BigDecimal decimalValue = new BigDecimal("2.345");

// Perbedaan presisi akan terlihat pada operasi yang melibatkan banyak digit desimal.

Representasi Bilangan dan Pembulatan

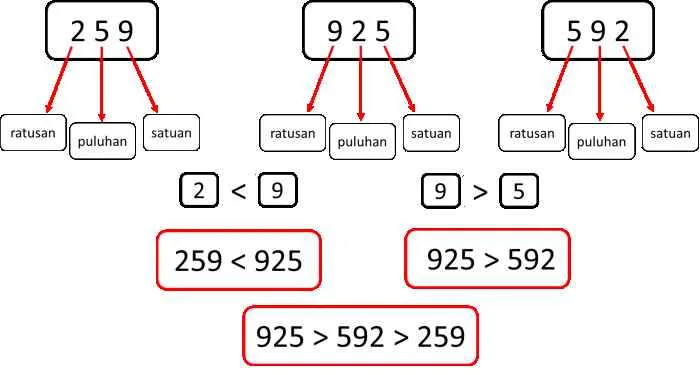
Pernahkah kamu bertanya-tanya kenapa hasil perhitungan di komputer terkadang sedikit berbeda dari yang diharapkan? Jawabannya mungkin terletak pada bagaimana komputer merepresentasikan bilangan, khususnya bilangan desimal. Artikel ini akan mengupas tuntas representasi bilangan titik mengambang dan dampaknya terhadap akurasi pembulatan, termasuk strategi untuk meminimalisir kesalahan yang mungkin terjadi.

Representasi Bilangan Titik Mengambang IEEE 754

Komputer menyimpan bilangan titik mengambang (seperti 3.14 atau -2.718) menggunakan standar IEEE 754. Standar ini membagi bilangan menjadi tiga bagian: tanda (sign), mantisa (significand), dan eksponen. Mantisa merepresentasikan angka signifikan, eksponen menentukan besarnya angka (skala), dan tanda menunjukkan apakah angka tersebut positif atau negatif. IEEE 754 memiliki dua presisi umum: single precision (32-bit) dan double precision (64-bit). Double precision menawarkan akurasi yang lebih tinggi karena memiliki lebih banyak bit untuk mantisa dan eksponen. Eksponen biasanya direpresentasikan dengan bias untuk memudahkan perhitungan dan representasi. Perbedaan jumlah bit ini langsung mempengaruhi akurasi pembulatan.

Contoh Kesalahan Pembulatan

Representasi bilangan titik mengambang seringkali menyebabkan kesalahan pembulatan. Berikut beberapa contohnya:

1. Penjumlahan Bilangan Kecil: Misalnya, menjumlahkan 0.000000001 + 0.000000001 + 0.000000001 sepuluh kali. Hasil yang diharapkan adalah 0.00000001, tetapi karena keterbatasan presisi, hasil yang didapat mungkin sedikit lebih kecil atau lebih besar. Ini disebabkan oleh pemotongan bit yang terjadi selama representasi bilangan dalam memori komputer.
2. Pengurangan Dua Bilangan yang Hampir Sama: Pertimbangkan 10000000000.000001 – 10000000000. Hasil yang diharapkan adalah 0.000001, tetapi karena representasi biner dari kedua angka hampir identik, perbedaannya bisa hilang selama perhitungan, menghasilkan kesalahan yang signifikan secara relatif.
3. Perkalian dan Pembagian: Hitung (10.0 / 3.0) * 3.0. Hasil yang diharapkan adalah 10.0, tetapi karena 10.0 / 3.0 tidak dapat direpresentasikan secara tepat dalam bilangan biner, hasilnya akan sedikit berbeda dari 10.0, dan perkalian selanjutnya akan memperbesar kesalahan tersebut.

Perbandingan Pembulatan Desimal dan Biner

Nilai Asli	Representasi Desimal (10 digit)	Representasi Biner (Single Precision)	Pembulatan Desimal	Pembulatan Biner
π	3.141592654	3.1415927410125732	3.141592654	3.14159274
√2	1.414213562	1.4142135623730951	1.414213562	1.4142136
1/3	0.3333333333	0.3333333432674408	0.3333333333	0.33333334
0.1	0.1	0.10000000149011612	0.1	0.1
0.0000000001	0.0000000001	0.00000000009313225746154785	0.0000000001	0.0000000001

Pentingnya Memahami Representasi Bilangan dalam Pembulatan

Memahami representasi bilangan sangat krusial, terutama dalam aplikasi yang sensitif terhadap kesalahan pembulatan seperti simulasi ilmiah, pemrosesan gambar, dan keuangan. Kesalahan pembulatan yang terakumulasi dapat menghasilkan hasil yang tidak akurat, bahkan bencana. Misalnya, kesalahan kecil dalam perhitungan trajektori pesawat ruang angkasa bisa berakibat fatal. Begitu pula dalam sistem keuangan, kesalahan pembulatan yang tidak terkendali bisa menyebabkan kerugian finansial yang besar.

Strategi Penanganan Kesalahan Pembulatan

Ada beberapa strategi untuk mengurangi dampak kesalahan pembulatan:

• Pilih tipe data yang tepat: Gunakan double jika akurasi tinggi diperlukan.
• Gunakan teknik pembulatan yang tepat: Pilih metode pembulatan yang sesuai dengan konteks masalah (pembulatan ke atas, ke bawah, atau ke angka terdekat).
• Gunakan library atau fungsi khusus: Beberapa library menyediakan fungsi untuk operasi aritmatika yang lebih akurat.
• Implementasi algoritma yang lebih stabil secara numerik: Algoritma tertentu lebih rentan terhadap akumulasi kesalahan daripada yang lain. Pilih algoritma yang lebih stabil.

Contoh Kode Python untuk Illustrasi

Berikut contoh kode Python yang menunjukkan penjumlahan 0.1 + 0.2 dengan dan tanpa strategi penanganan kesalahan pembulatan (menggunakan library decimal untuk akurasi yang lebih tinggi):

import decimal

# Tanpa penanganan kesalahan
hasil_biasa = 0.1 + 0.2
print(f"Hasil biasa: hasil_biasa")

# Dengan penanganan kesalahan menggunakan decimal
context = decimal.Context(prec=10) # prec menentukan presisi
decimal.setcontext(context)
hasil_decimal = decimal.Decimal("0.1") + decimal.Decimal("0.2")
print(f"Hasil dengan decimal: hasil_decimal")

Pembulatan dan Kesalahan Pembulatan

Pernah ngerjain soal matematika, terus hasilnya angka desimal panjang banget? Ribet kan? Nah, di situlah pentingnya pembulatan. Tapi, tau nggak sih, pebulatan itu bisa bikin hasil perhitungan kita meleset sedikit? Yup, itu yang disebut kesalahan pembulatan. Artikel ini akan bahas tuntas tentang konsep kesalahan pembulatan, bagaimana menghitungnya, dan cara meminimalisir dampaknya.

Kesalahan Pembulatan

Kesalahan pembulatan adalah selisih antara nilai sebenarnya dan nilai yang sudah dibulatkan. Semakin banyak angka desimal yang dihilangkan saat pembulatan, semakin besar potensi kesalahan yang terjadi. Bayangkan kamu lagi ngitung luas lahan, sedikit saja kesalahan pembulatan bisa bikin perhitungan luas lahan jadi meleset jauh!

Contoh Perhitungan Kesalahan Pembulatan

Misalnya, kita punya angka 3,14159. Kalau dibulatkan ke dua angka desimal, hasilnya 3,14. Kesalahan pembulatannya adalah 3,14159 – 3,14 = 0,00159. Kelihatannya kecil, tapi coba bayangkan kalau angka ini dikalikan dengan angka yang besar, kesalahan pembulatannya juga akan membesar.

Hubungan Jumlah Angka Desimal dan Kesalahan Pembulatan

Jumlah Angka Desimal	Nilai yang Dibulatkan (dari 3,14159)	Kesalahan Pembulatan
0	3	0,14159
1	3,1	0,04159
2	3,14	0,00159
3	3,142	-0,00041

Tabel di atas menunjukkan bahwa semakin banyak angka desimal yang dipertahankan, semakin kecil kesalahan pembulatannya. Perhatikan bahwa kesalahan bisa positif (nilai dibulatkan lebih kecil dari nilai sebenarnya) atau negatif (nilai dibulatkan lebih besar dari nilai sebenarnya).

Cara Meminimalisir Kesalahan Pembulatan

Ada beberapa cara untuk meminimalisir kesalahan pembulatan. Pertama, gunakan sebanyak mungkin angka desimal selama perhitungan. Kedua, lakukan pembulatan hanya pada tahap akhir perhitungan. Ketiga, gunakan metode pembulatan yang tepat, seperti pembulatan ke atas, ke bawah, atau pembulatan setengah ke atas, sesuai kebutuhan perhitungan.

Metode Estimasi Kesalahan Pembulatan

Besarnya kesalahan pembulatan bisa diestimasi dengan melihat angka desimal pertama yang dihilangkan. Misalnya, jika kita membulatkan 3,14159 ke 3,14, maka kesalahan pembulatannya kira-kira sebesar setengah dari nilai tempat desimal yang dihilangkan, yaitu 0,0005. Metode ini memberikan estimasi kasar, tapi cukup berguna untuk mendapatkan gambaran umum besarnya kesalahan.

Penutupan Akhir

Jadi, 5,29 dibulatkan menjadi berapa? Jawabannya bergantung pada metode pembulatan yang dipilih dan konteksnya. Memahami berbagai metode pembulatan dan aturannya sangat penting untuk memastikan keakuratan hasil perhitungan, baik dalam kehidupan sehari-hari maupun dalam konteks yang lebih kompleks seperti keuangan dan ilmu pengetahuan. Jangan sampai salah bulatkan, ya! Semoga artikel ini membantu Anda memahami lebih dalam tentang seni membulatkan angka.